Góc thân mật nhị mặt mũi bằng...
1. Góc thân mật nhị mặt mũi bằng.
Định nghĩa: Góc thân mật nhị mặt mũi bằng là góc thân mật hai tuyến phố trực tiếp theo thứ tự vuông góc với nhị mặt mũi bằng cơ.
Bạn đang xem: 2 mặt phẳng vuông góc
Cách xác lập góc thân mật nhị mặt mũi phẳng:
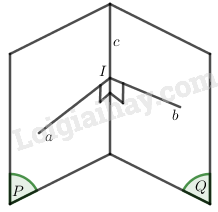
\((P) ∩ (Q) = c\). Trong \((P)\) kể từ \(I ∈ c\) vẽ \(a ⊥ c\); nhập \((Q)\) kể từ \(I\) vẽ \(b ⊥ c\). Góc thân mật \(a\) và \(b\) là góc thân mật \(mp(P)\) và \(mp(Q)\) (h.3.41).
Diện tích hình chiếu của một nhiều giác.
Cho nhiều giác \(H\) nằm trong \(mp(Q)\). Gọi nhiều giác \(H'\) là hình chiếu của nhiều giác \(H\) lên \(mp(P)\); \(α = \widehat{(P; Q)}.\) Khi đó \(S_{H'}=S_{H}.cos\alpha .\)
2. Hai mặt mũi bằng vuông góc
Định nghĩa:
Hai mặt mũi bằng gọi là vuông góc cùng nhau nếu như góc thân mật bọn chúng vị \(90^{0}.\)
Định lý: Điều khiếu nại cần thiết và đầy đủ nhằm nhị mặt mũi bằng vuông góc cùng nhau là mặt mũi bằng này chứa một đường thẳng liền mạch vuông góc với mặt mũi bằng kia.
Hệ trái khoáy 1
Nếu nhị mặt mũi bằng \((P)\) và \((Q)\) vuông góc cùng nhau thì bất kể đường thẳng liền mạch \(a\) này nằm trong mặt mũi bằng \((P)\), vuông góc với gửi gắm tuyến của \((P)\) và \((Q)\) đều vuông góc với mp \((Q)\).
Hệ trái khoáy 2
Nếu nhị mặt mũi bằng \((P)\) và \((Q)\) vuông góc cùng nhau và \(A\) là 1 trong những điểm nằm trong \((P)\) thì đường thẳng liền mạch \(a\) trải qua điểm \(A\) và vuông góc với \((Q)\) tiếp tục nằm trong \((P)\).
Hệ trái khoáy 3
Nếu nhị mặt mũi bằng tách nhau và nằm trong vuông góc với mặt mũi bằng loại thân phụ thì gửi gắm tuyến của bọn chúng vuông góc với mặt mũi bằng loại thân phụ.
3. Hình lăng trụ đứng, hình vỏ hộp chữ nhật, hình lập phương.
. Hình lăng trụ đứng là hình lăng trụ đứng sở hữu lòng là nhiều giác đều.
. Hình vỏ hộp đứng là hình lăng trụ đứng sở hữu lòng là hình bình hành.
. Hình vỏ hộp chữ nhật là hình vỏ hộp đứng sở hữu đấy là hình chữ nhật.
Xem thêm: công thức tính tỉ lệ gia tăng tự nhiên
. Hình lập phương là hình vỏ hộp sở hữu toàn bộ những mặt mũi là hình vuông vắn.
4. Hình chóp đều và hình chóp cụt đều.
Hình chóp đều:
- Một hình chóp được gọi là hình chóp đều nếu như lòng của chính nó là một trong nhiều giác đều và đàng cao của hình chóp trải qua tâm của đấy.
- Hình chóp đều sở hữu những mặt mũi cạnh mặt mũi tạo ra với mặt mũi lòng những góc cân nhau.
Hình chóp cụt đều:
Phần nằm trong lòng lòng và một tiết diện tuy vậy song với lòng của hình chóp đều gọi là hình chóp cụt đều.
Loigiaihay.com
Bình luận
![]() Chia sẻ
Chia sẻ
-
Câu căn vặn 1 trang 109 SGK Hình học tập 11
Cho nhị mặt mũi bằng (α) và (β) vuông góc cùng nhau và tách nhau theo đòi gửi gắm tuyến d....
-
Câu căn vặn 2 trang 109 SGK Hình học tập 11
Cho tứ diện ABCD sở hữu thân phụ cạnh AB, AC, AD song một vuông góc cùng nhau....
-
Câu căn vặn 3 trang 109 SGK Hình học tập 11
Cho hình vuông vắn ABCD. Dựng đoạn AS vuông góc với mặt mũi bằng chứa chấp hình vuông vắn ABCD...
-
Câu căn vặn 4 trang 111 SGK Hình học tập 11
Giải thắc mắc 4 trang 111 SGK Hình học tập 11. Cho biết mệnh đề này sau đó là đích ?...
-
Câu căn vặn 5 trang 111 SGK Hình học tập 11
Giải thắc mắc 5 trang 111 SGK Hình học tập 11. Sáu mặt mũi của hình vỏ hộp chữ nhật liệu có phải là những hình chữ nhật ko ?...
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Xem thêm: cách tính hiệu suất phản ứng
2k7 Tham gia tức thì group share, trao thay đổi tư liệu học hành mễn phí

>> Học trực tuyến Lớp 11 bên trên Tuyensinh247.com. Cam kết chung học viên lớp 11 học tập đảm bảo chất lượng, trả trả ngân sách học phí nếu như học tập ko hiệu suất cao.













Bình luận