Chủ đề tình huống đều bằng nhau của tam giác vuông: Tam giác vuông có tương đối nhiều tình huống đều bằng nhau, điều này tạo cho tam giác vuông trở thành thú vị và nhiều mẫu mã. Có nhị tình huống cần thiết nhằm Note là lúc nhị cạnh góc vuông của tam giác vuông đều bằng nhau và khi cạnh góc vuông và góc nhọn kề cạnh này cũng đều bằng nhau. Việc dò thám hiểu và vận dụng những tình huống này gom tất cả chúng ta nắm rõ rộng lớn về đặc điểm quan trọng đặc biệt của tam giác vuông và xử lý những vấn đề tương quan cho tới nó một cơ hội dễ dàng và đơn giản.
Có những tình huống nào là khiến cho nhị tam giác vuông trở thành bởi vì nhau?
Có những tình huống thực hiện mang lại nhị tam giác vuông trở thành bởi vì nhau:
1. Trường hợp ý 1: Hai cạnh góc vuông của nhị tam giác vuông đều bằng nhau. Vấn đề này Tức là nhị tam giác vuông có tính lâu năm nhị cạnh góc vuông đều đều bằng nhau.
2. Trường hợp ý 2: Một cạnh góc vuông và một góc nhọn kề cạnh cơ của nhị tam giác vuông đều bằng nhau. Vấn đề này Tức là nhị tam giác vuông với cùng một cạnh góc vuông và một góc nhọn kề cạnh cơ có tính lâu năm đều bằng nhau.
3. Trường hợp ý 3: Cạnh huyền và một cạnh góc vuông của nhị tam giác vuông đều bằng nhau. Vấn đề này Tức là nhị tam giác vuông với cạnh huyền và một cạnh góc vuông có tính lâu năm đều bằng nhau.
Để xác nhận rằng nhị tam giác vuông đều bằng nhau, tao cần thiết xác minh rằng những cạnh và góc ứng của nhị tam giác và đã được hướng đẫn trong số tình huống bên trên đều đều bằng nhau.
Bạn đang xem: các trường hợp bằng nhau của tam giác vuông
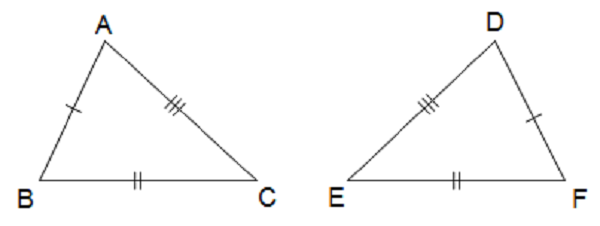
Trường hợp ý nào là khi nhị tam giác vuông sẽ là bởi vì nhau?
Trường hợp ý khi nhị tam giác vuông sẽ là đều bằng nhau là lúc những cạnh góc vuông và cạnh huyền của nhị tam giác vuông này đều bằng nhau.
Cụ thể, với nhị tình huống khi nhị tam giác vuông sẽ là bởi vì nhau:
Trường hợp ý 1: Hai cạnh góc vuông của nhị tam giác vuông bởi vì nhau: Trong tình huống này, nhị tam giác vuông sẽ có được nhị cạnh góc vuông có tính lâu năm đều bằng nhau.
Trường hợp ý 2: Cạnh góc vuông và góc nhọn kề cạnh góc vuông của nhị tam giác vuông bởi vì nhau: Trong tình huống này, một cạnh góc vuông của tam giác vuông trước tiên và góc nhọn kề cạnh góc vuông này cũng bởi vì cạnh ứng của tam giác vuông loại nhị.
Khi nhị tam giác vuông thỏa mãn nhu cầu 1 trong các nhị tình huống bên trên, bọn chúng sẽ là đều bằng nhau. Vấn đề này đồng nghĩa tương quan với việc những góc, cạnh và cạnh huyền ứng của nhị tam giác vuông đều bằng nhau.
Có từng nào tình huống đều bằng nhau của tam giác vuông?
Có nhị tình huống đều bằng nhau của tam giác vuông.
1. Trường hợp ý 1: Hai cạnh góc vuông của nhị tam giác vuông đều bằng nhau.
2. Trường hợp ý 2: Một cạnh góc vuông và cạnh kề góc vuông của nhị tam giác vuông đều bằng nhau.
Tam giác vuông - Bài 8 - Toán học tập 7 - Cô Nguyễn Anh (HAY NHẤT)
Tại sao tình huống đều bằng nhau lại cần thiết nhập toán học? Video này tiếp tục lý giải một cơ hội rõ rệt và sáng tỏ, giúp đỡ bạn hiểu đích và vận dụng công thức một cơ hội đúng mực. Hãy coi tức thì nhằm nắm rõ loài kiến thức!
Tam giác vuông đều bằng nhau khi nào?
Tam giác vuông đều bằng nhau khi nhị tam giác vuông này còn có nằm trong cạnh huyền và và một cạnh góc vuông.
Cụ thể, với nhị tình huống khi tam giác vuông bởi vì nhau:
1. Trường hợp ý 1: Hai tam giác vuông với cạnh góc vuông chung:
- Nếu nhị tam giác vuông với cạnh góc vuông công cộng, tức là một trong cạnh góc vuông và một cạnh huyền của tam giác vuông này bởi vì một cạnh góc vuông và một cạnh huyền của tam giác vuông cơ, thì nhị tam giác vuông cơ đều bằng nhau.
2. Trường hợp ý 2: Hai tam giác vuông với cạnh góc vuông ko công cộng tuy nhiên cạnh huyền chung:
- Nếu nhị tam giác vuông với cạnh huyền công cộng, tức là cạnh huyền và một cạnh góc vuông của tam giác vuông này bởi vì cạnh huyền và một cạnh góc vuông của tam giác vuông cơ, thì nhị tam giác vuông cơ đều bằng nhau.
Đó là cơ hội xác lập lúc nào nhị tam giác vuông đều bằng nhau dựa vào cạnh huyền và cạnh góc vuông của bọn chúng.
Tam giác vuông đều bằng nhau với những Đặc điểm gì?
Tam giác vuông đều bằng nhau với những Đặc điểm sau:
1. Hai tam giác vuông được gọi là đều bằng nhau nếu như một cạnh của góc vuông và cạnh huyền của tam giác vuông này bởi vì một cạnh của góc vuông và cạnh huyền của tam giác vuông cơ.
2. Trường hợp ý 1: Hai tam giác vuông với nhị cạnh góc vuông đều bằng nhau (đối đối với cả nhị góc vuông).
3. Trường hợp ý 2: Hai tam giác vuông với cùng một cạnh góc vuông và góc nhọn kề cạnh cơ đều bằng nhau.
4. Hai tam giác vuông đều bằng nhau cũng đều có những cặp cạnh ứng đều bằng nhau, chính vì cạnh huyền của tam giác vuông đó là cạnh lớn số 1 và đối lập với góc vuông.
_HOOK_
Tam giác vuông - Phần 1 - Toán 7 - OLM.VN
Bạn đang được học tập toán học tập lớp 7 và ham muốn nâng cấp khả năng của mình? Video này tiếp tục hỗ trợ những bài bác giảng và ví dụ thực tiễn giúp đỡ bạn nắm rõ rộng lớn về những chủ thể phức tạp như hình học tập, cách thức giải toán. Hãy nằm trong học tập và băng qua những thách thức!
Xem thêm: silic là kim loại hay phi kim
Các tình huống đều bằng nhau của tam giác vuông khi với cạnh góc vuông và góc nhọn là gì?
Các tình huống đều bằng nhau của tam giác vuông khi với cạnh góc vuông và góc nhọn là như sau:
1. Trường hợp ý 1: Hai cạnh góc vuông đều bằng nhau.
Khi nhị tam giác vuông với cạnh góc vuông đều bằng nhau, tao với tam giác vuông này là đều bằng nhau.
2. Trường hợp ý 2: Cạnh góc vuông và góc nhọn kề cạnh cơ đều bằng nhau.
Khi nhị tam giác vuông với cạnh góc vuông và góc nhọn kề cạnh cơ đều bằng nhau, tao với tam giác vuông này là đều bằng nhau.
Ví dụ:
Cho nhị tam giác vuông ABC và DEF. Ta biết AB = DE và góc A = góc D. Khi cơ, tam giác ABC và tam giác DEF là đều bằng nhau.
Đây là những tình huống cơ phiên bản nhằm xác lập nhị tam giác vuông với đều bằng nhau hay là không, dựa vào đặc điểm của cạnh góc vuông và góc nhọn.
Trường hợp ý nào là là tình huống một trong những các trường hợp bằng nhau của tam giác vuông?
Trường hợp ý một trong những các trường hợp bằng nhau của tam giác vuông là lúc nhị tam giác vuông với nhị cạnh góc vuông đều bằng nhau. Để tình huống này xẩy ra, tao cần thiết đối chiếu phỏng lâu năm nhị cạnh góc vuông của nhị tam giác và xác lập coi bọn chúng với đều bằng nhau ko. Nếu nhị cạnh góc vuông của nhị tam giác có tính lâu năm như nhau, tức là cạnh này của tam giác loại nhất có tính lâu năm bởi vì cạnh ứng của tam giác loại nhị, thì cơ đó là tình huống một trong những các trường hợp bằng nhau của tam giác vuông.

Trong tình huống 2, tam giác vuông đều bằng nhau khi với cạnh góc vuông và góc nhọn kề cạnh cơ như vậy nào?
Trong tình huống 2 của tam giác vuông đều bằng nhau, tất cả chúng ta với cùng một cạnh góc vuông và góc nhọn kề cạnh cơ. Để tam giác vuông đều bằng nhau, cạnh góc vuông và góc nhọn kề cạnh cơ của nhị tam giác rất cần được tương tự.
Để xác lập nhị tam giác với tương tự hay là không, tất cả chúng ta cần thiết đối chiếu những nhân tố sau:
1. Cạnh góc vuông: Hai tam giác cần phải có cạnh góc vuông đều bằng nhau. Vấn đề này Tức là cạnh góc vuông của tam giác A cần bởi vì cạnh góc vuông của tam giác B.
2. Góc nhọn kề cạnh đó: Cả nhị tam giác cần phải có góc nhọn kề cạnh cơ tương tự. Vấn đề này Tức là góc nhọn kề cạnh cơ của tam giác A cần bởi vì góc nhọn kề cạnh cơ của tam giác B.
Nếu cả nhị nhân tố này đều thoả mãn, tức là cạnh góc vuông và góc nhọn kề cạnh cơ của nhị tam giác đều bằng nhau, thì tao rất có thể Kết luận rằng nhị tam giác này là tương tự và đều bằng nhau.
Ví dụ:
Tam giác A với cạnh góc vuông AB và góc nhọn kề cạnh cơ AC.
Tam giác B với cạnh góc vuông DE và góc nhọn kề cạnh cơ DF.
Nếu AB = DE và AC = DF, thì tao rất có thể Kết luận rằng tam giác A và tam giác B là tương tự và đều bằng nhau.
Tam giác vuông - Bài 8 - Toán học tập 7 - Cô Nguyễn Thu Hà (DỄ HIỂU NHẤT)
Cô Nguyễn Anh là một trong nhà giáo toán tài năng và hăng hái. Video này tiếp tục mang về những bài bác giảng trải qua cách thức giảng dạy dỗ lạ mắt của cô ý. Hãy lắng tai những lời nói giảng kể từ cô nhằm thâu tóm kiến thức và kỹ năng một cơ hội dễ dàng và đơn giản và thú vị!
Cách đánh giá và minh chứng nhị tam giác vuông đều bằng nhau như vậy nào?
Để đánh giá và minh chứng nhị tam giác vuông đều bằng nhau, tất cả chúng ta rất có thể dùng một trong mỗi cơ hội sau:
Cách 1: Sử dụng phép tắc té đề. Để thực hiện điều này, tất cả chúng ta cần thiết minh chứng rằng nhị tam giác vuông với và một cặp cạnh góc vuông và cạnh huyền. Cụ thể, tao rất có thể tiến hành quá trình sau:
Bước 1: Xác tấp tểnh những cặp cạnh góc vuông và cạnh huyền của nhị tam giác vuông cần thiết minh chứng.
Bước 2: So sánh những cặp cạnh góc vuông và cạnh huyền của nhị tam giác. Nếu bọn chúng đều bằng nhau, tao rất có thể Kết luận nhị tam giác vuông cơ đều bằng nhau.
Cách 2: Sử dụng giải tích hình học tập. Đối với tình huống này, tất cả chúng ta cần thiết minh chứng rằng những góc và phỏng lâu năm những cạnh của nhị tam giác vuông đều bằng nhau.
Bước 1: Gán độ quý hiếm cho những đỉnh của nhị tam giác vuông.
Bước 2: Tính toán những góc và phỏng lâu năm những cạnh của tất cả nhị tam giác.
Bước 3: So sánh những góc và phỏng lâu năm những cạnh của nhị tam giác. Nếu bọn chúng đều bằng nhau, tao rất có thể Kết luận nhị tam giác vuông cơ đều bằng nhau.
Đối đối với cả nhị cơ hội bên trên, tất cả chúng ta cần thiết xem xét đảm nói rằng toàn bộ những độ quý hiếm được xem toán và đối chiếu đều đúng mực. Nếu những độ quý hiếm tương đương nhau, tao rất có thể Kết luận rằng những tam giác vuông là đều bằng nhau.
Xem thêm: bộ sách chân trời sáng tạo

Tại sao việc hiểu về những tình huống đều bằng nhau của tam giác vuông cần thiết nhập học tập hình học?
Việc hiểu về những tình huống đều bằng nhau của tam giác vuông là đặc biệt cần thiết nhập học tập hình học tập vì như thế nó gom tất cả chúng ta thấy được côn trùng contact Một trong những Đặc điểm và đặc điểm của những tam giác vuông không giống nhau.
1. Trường hợp ý cạnh góc vuông: Khi nhị tam giác vuông với cạnh góc vuông đều bằng nhau, tao rất có thể Kết luận rằng những cạnh còn sót lại cũng tiếp tục đều bằng nhau. Vấn đề này thể hiện một quy tắc cần thiết nhập hình học tập là: \"Hai tam giác vuông với cùng một cặp cạnh đều bằng nhau thì những cặp cạnh còn sót lại cũng đều bằng nhau.\"
2. Trường hợp ý cạnh góc vuông và góc nhọn kề cạnh đó: Nếu một cạnh góc vuông và góc nhọn kề cạnh cơ của nhị tam giác vuông đều bằng nhau, tao rất có thể Kết luận rằng tam giác vuông này cũng đều bằng nhau. Vấn đề này được chấp nhận tất cả chúng ta vận dụng quy tắc về những lối cao, trung tuyến, lối khoảng và những nhân tố không giống nhập tam giác vuông.
3. Trường hợp ý cạnh huyền và cạnh góc vuông: Nếu cạnh huyền và một cạnh góc vuông của nhị tam giác vuông đều bằng nhau, thì tao rất có thể Kết luận rằng những tam giác vuông cơ đều bằng nhau. Vấn đề này gom tất cả chúng ta xác lập những cặp góc đều bằng nhau và ĐK chắc chắn trong số tam giác vuông.
Bằng cơ hội nắm rõ những tình huống đều bằng nhau này, tất cả chúng ta rất có thể vận dụng những cách thức, công thức và tấp tểnh lý nhằm xử lý những bài bác tập luyện và yếu tố tương quan cho tới tam giác vuông. Trong khi, việc hiểu sâu sắc về những tình huống này còn rất có thể gom tất cả chúng ta cải tiến và phát triển năng lực trí tuệ, logic và xử lý yếu tố nhập hình học tập.
_HOOK_











Bình luận