hệ số góc của đường thẳng

By Admin 16/12/2023 0

Gọi A là uỷ thác điểm của lối thẳng

Tổng phù hợp đề ganh đua học tập kì 1 lớp 9 toàn bộ những môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Bạn đang xem: hệ số góc của đường thẳng

1. Góc tạo nên vì chưng đường thẳng liền mạch \(y = ax + b (a ≠ 0)\) và trục \(Ox.\)

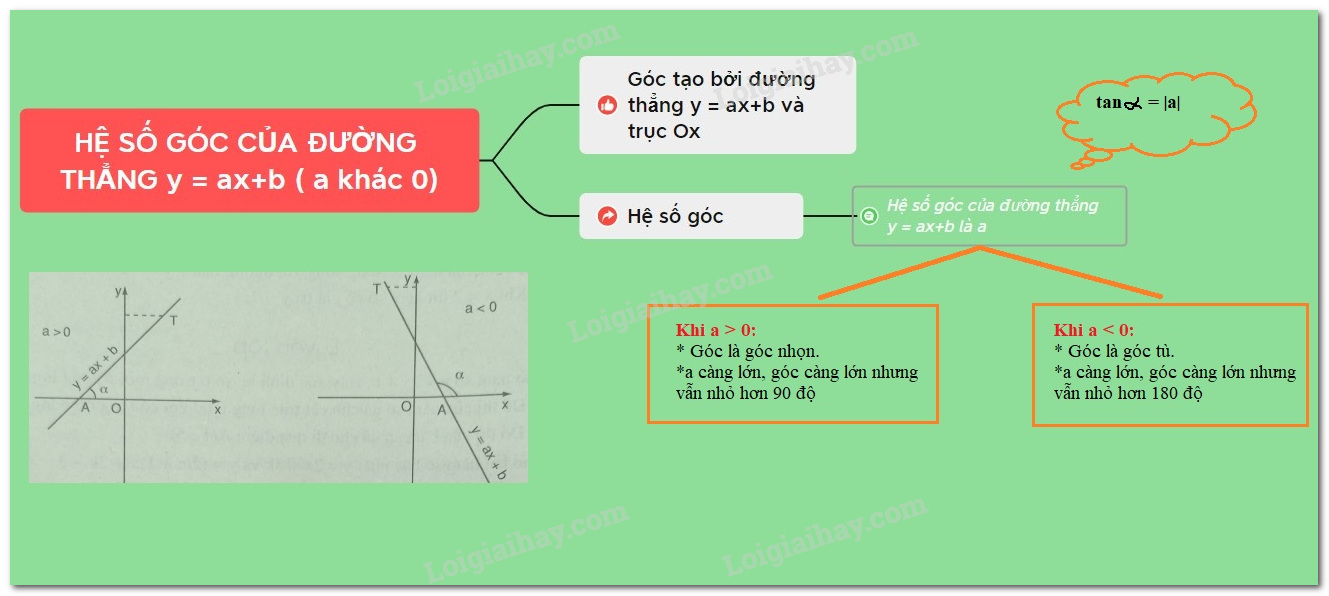
Gọi \(A\) là uỷ thác điểm của đường thẳng liền mạch \(d:y = ax + b\) với trục \(Ox\) và \(T\) là một trong những điểm nằm trong đường thẳng liền mạch, ở phía bên trên trục \(Ox.\) Khi cơ góc \(\alpha=\widehat {TAx}\) được gọi là góc tạo nên vì chưng đường thẳng liền mạch \(d: nó = ax + b\) và trục \(Ox.\) 

 

2. Hệ số góc của đường thẳng liền mạch \(y = ax + b (a ≠ 0)\) 

+) Khi \(a > 0,\) góc tạo nên vì chưng đường thẳng liền mạch \(y = ax + b\) và trục \(Ox\) là góc nhọn và nếu như \(a\) càng rộng lớn thì góc cơ càng rộng lớn vẫn nhỏ rộng lớn \(90^0.\)

+) Khi \(a < 0,\) góc tạo nên vì chưng đường thẳng liền mạch \(y = ax + b\) và trục \(Ox\) là góc tù và nếu như \(|a|\) càng bé bỏng thì góc cơ càng rộng lớn vẫn nhỏ rộng lớn \(180^0.\)

Như vậy, góc tạo nên vì chưng đường thẳng liền mạch \(d: nó = ax + b\) và trục \(Ox\) tùy thuộc vào \(a.\)

Người tớ gọi \(a\) là hệ số góc của đường thẳng liền mạch \(y = ax + b.\)

Lưu ý:

+) Khi \(a > 0,\) tớ sở hữu \(\tan \alpha= a.\)

+) Khi \(a < 0,\) tớ sở hữu \(\tan (180^0-\alpha) = -a.\)

Từ cơ tìm kiếm được số đo của góc \(180^0-\alpha\) rồi suy đi ra số đo của góc \(\alpha.\)

+) Các đường thẳng liền mạch sở hữu nằm trong thông số \(a\) (\(a\) là thông số của \(x\)) thì tạo nên với trục \(Ox\) những góc đều nhau.

3. Các dạng toán cơ bản

Dạng 1: Xác toan hệ số góc của đường thẳng

Phương pháp:

Đường trực tiếp \((d)\) sở hữu phương trình \(y = ax + b\,\left( {a \ne 0} \right)\) sở hữu \(a\) là thông số góc.

Ví dụ: Hệ số góc của đường thẳng liền mạch \(y=-2x+1\) là \(a=-2\)

Dạng 2: Tính góc tạo nên vì chưng tia \(Ox\) và đường thẳng liền mạch \((d).\)

Phương pháp:

Xem thêm: tính oxi hóa là gì

Gọi \(\alpha \) là góc tạo nên vì chưng tia \(Ox\) và \(d.\) Ta có: \(a = \tan \alpha \)

Ví dụ: Góc tạo nên vì chưng tia \(Ox\) và đường thẳng liền mạch \((d):y=\sqrt 3 x+1\) là \(\alpha \)

Khi đó: \(\tan \alpha=\sqrt 3\) nên \(\alpha =60^0\)

Dạng 3. Viết phương trình đường thẳng liền mạch hoặc thám thính thông số m lúc biết thông số góc

Phương pháp:

Gọi phương trình  đường trực tiếp cần thiết thám thính là $y = ax + b\,\,\left( {a \ne 0} \right)$.

Dựa vô lý thuyết về thông số góc nhằm tìm $a$. Từ cơ, dùng dữ khiếu nại còn sót lại của đề bài xích nhằm tìm $b$.


Bình luận

Chia sẻ

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Xem thêm: bác hồ bao nhiêu tuổi

Báo lỗi - Góp ý

Tham Gia Group 2K9 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến lớp 9 và luyện vô lớp 10 bên trên Tuyensinh247.com, khẳng định gom học viên lớp 9 học tập đảm bảo chất lượng, trả trả tiền học phí nếu như học tập ko hiệu suất cao.