Chủ đề Cách nhằm minh chứng hình thoi: Có nhiều phương pháp để minh chứng một tứ giác là hình thoi. Trước hết, nếu như tứ giác sở hữu tư cạnh đều bằng nhau, thì nó là hình thoi. Dường như, nếu như tứ giác sở hữu 2 lối chéo cánh là lối trung trực của nhau, cũng chứng minh này đó là hình thoi. Hình như, những đặc thù của hình bình hành cũng vận dụng mang đến hình thoi. Tất cả những cơ hội minh chứng này canh ty học viên nắm rõ và phần mềm chất lượng tốt định nghĩa hình thoi.
Các cách thức minh chứng hình thoi là gì?
Có phụ thân cách thức minh chứng một tứ giác là hình thoi như sau:
Phương pháp 1: Tứ giác sở hữu tư cạnh bởi vì nhau
- Cho tứ giác ABCD, với AB = BC = CD = DA.
- Cần minh chứng tứ giác ABCD là hình thoi.
- Ta dùng công thức khoảng cách Euclid nhằm minh chứng rằng tứ giác này là hình thoi.
- Khi hai tuyến đường chéo cánh AC và BD tách nhau bên trên O, tao tính khoảng cách kể từ O cho tới những đỉnh và đối chiếu nếu như toàn bộ đều bằng nhau thì tứ giác là hình thoi.
Phương pháp 2: Tứ giác sở hữu 2 lối chéo cánh là lối trung trực của nhau
- Cho tứ giác ABCD, với AC là lối chéo cánh phân chia tứ giác trở thành nhì tam giác quá.
- Cần minh chứng tứ giác ABCD là hình thoi.
- Ta dùng công thức tính diện tích S tam giác nhằm minh chứng rằng tứ giác này là hình thoi.
- Nếu diện tích S nhì tam giác quá đều bằng nhau, tứ giác là hình thoi.
Phương pháp 3: Hình thoi là tứ giác sở hữu nhì cạnh kề đều bằng nhau và nhì góc kề bởi vì nhau
- Cho tứ giác ABCD, với AB = BC và góc BAC = góc BCD.
- Cần minh chứng tứ giác ABCD là hình thoi.
- Ta dùng công thức tính phỏng lâu năm cạnh và góc nhằm minh chứng rằng tứ giác này là hình thoi.
- Nếu nhì cạnh kề đều bằng nhau và nhì góc kề đều bằng nhau, tứ giác là hình thoi.
Lưu ý: Đối với từng cách thức, cần thiết đánh giá và xác nhận ĐK của cách thức trước lúc tiếp cận tóm lại rằng tứ giác là hình thoi.
Bạn đang xem: cách chứng minh hình thoi
Hình thoi sở hữu từng nào đặc thù tương tự với hình bình hành?
Hình thoi sở hữu những đặc thù tương tự với hình bình hành như sau:
1. Có cạnh đối tuy nhiên song và bởi vì nhau: Như vậy Có nghĩa là cặp cạnh đối lập của hình thoi là tuy nhiên song và có tính lâu năm đều bằng nhau.
2. Có những góc đối bởi vì nhau: Hình thoi sở hữu nhì cặp góc đối lập đều bằng nhau, sở hữu góc nhập đều bằng nhau và sở hữu góc ngoài đều bằng nhau.
3. Hai lối chéo cánh tách nhau vuông góc và phân chia hình thoi trở thành 4 tam giác đồng dạng: Đường chéo cánh của hình thoi tách nhau bên trên một điểm tuy nhiên giao phó điểm này đó là trung điểm của tất cả hai tuyến đường chéo cánh, và lối chéo cánh tách góc 90 phỏng cùng nhau. Hình như, lối chéo cánh phân chia hình thoi trở thành 4 tam giác đồng dạng.
Như vậy, hình thoi sở hữu 3 đặc thù tương tự với hình bình hành.
Tứ giác này được minh chứng là hình thoi nếu như sở hữu tư cạnh bởi vì nhau?
Để minh chứng một tứ giác là hình thoi, tao cần thiết cảm biến được rằng tứ giác bại sở hữu những cạnh đều bằng nhau. Dưới đấy là phương pháp để minh chứng một tứ giác là hình thoi nếu như sở hữu tư cạnh bởi vì nhau:
Bước 1: Đề rời khỏi fake thiết rằng tứ giác ABCD sở hữu tư cạnh đều bằng nhau. Ta fake sử cạnh AB = BC = CD = DA.
Bước 2: Chứng minh hai tuyến đường chéo cánh đều bằng nhau và tách nhau vuông góc.
- Ta cần thiết minh chứng rằng lối chéo cánh AC tách lối chéo cánh BD bên trên một điểm O và nhì đoạn OA và OC đều bằng nhau (AO = OC).
- Chứng minh nhì tam giác AOĐ và COB đồng dạng cùng nhau.
Bước 3: Kết luận rằng tứ giác ABCD là hình thoi dựa vào việc minh chứng được đối xứng tâm O và những cạnh đều bằng nhau.
Lưu ý: Đây chỉ là 1 trong những nhập số những cơ hội minh chứng một tứ giác là hình thoi, còn vô số cách thức không giống nhau tùy từng ĐK và fake thiết rõ ràng của vấn đề. Trên trên đây chỉ là 1 trong những ví dụ mang tính chất hóa học cộng đồng.
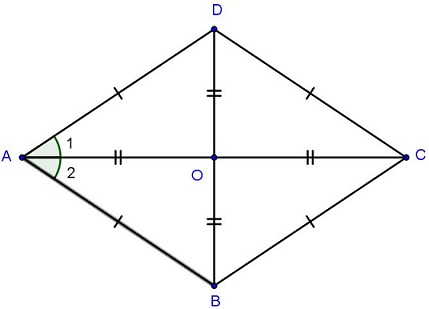
Điều khiếu nại này nhằm một tứ giác được minh chứng là hình thoi nếu như hai tuyến đường chéo cánh là lối trung trực của nhau?
Điều khiếu nại nhằm một tứ giác được minh chứng là hình thoi nếu như hai tuyến đường chéo cánh là lối trung trực của nhau giản dị và đơn giản là:
Bước 1: Xác lăm le tứ giác sở hữu hai tuyến đường chéo cánh là AB và CD.
Bước 2: Vẽ lối chéo cánh AC và BD.
Bước 3: Chứng minh rằng hai tuyến đường chéo cánh AB và CD là lối trung trực của nhau. Để minh chứng điều này, tao hoàn toàn có thể dùng một trong mỗi cơ hội sau đây:
a. Sử dụng đặc thù của hình thoi: Hai lối chéo cánh là lối trung trực của nhau.
b. Sử dụng đặc thù của tam giác: Chứng minh nhì tam giác vuông cân nặng Ngân Hàng Á Châu và ABD sở hữu cạnh và góc cộng đồng, dẫn theo hai tuyến đường chéo cánh là lối trung trực của nhau.
c. Sử dụng đặc thù của hình vuông: Chứng minh nhì tam giác vuông cân nặng Ngân Hàng Á Châu và ABD sở hữu cạnh và góc cộng đồng, dẫn theo hai tuyến đường chéo cánh là lối trung trực của nhau.
Bước 4: Khi đang được minh chứng được hai tuyến đường chéo cánh là lối trung trực của nhau, tao hoàn toàn có thể tóm lại rằng tứ giác ABCD là hình thoi.
Chú ý: Đây chỉ là 1 trong những trong mỗi cơ hội minh chứng tứ giác là hình thoi với ĐK hai tuyến đường chéo cánh là lối trung trực của nhau. Còn vô số cách thức minh chứng không giống nhau tuy nhiên chúng ta có thể mò mẫm hiểu thêm thắt.
Có bao nhiêu cơ hội minh chứng một tứ giác là hình thoi?
Có phụ thân cơ hội minh chứng một tứ giác là hình thoi.
Cách 1: Tứ giác sở hữu tư cạnh đều bằng nhau.
- Ta cần thiết minh chứng rằng cả tư cạnh của tứ giác đều đều bằng nhau.
- Sử dụng công thức khoảng cách thân mật nhì điểm nhập hệ trục toạ phỏng nhằm tính khoảng cách trong những đỉnh của tứ giác.
- Nếu tao thấy rằng cả tư cạnh đều sở hữu khoảng cách đều bằng nhau, tứ giác này đó là hình thoi.
Cách 2: Tứ giác sở hữu 2 lối chéo cánh là lối trung trực của nhau.
- Ta cần thiết minh chứng rằng hai tuyến đường chéo cánh của tứ giác tách nhau ở giao phó điểm là trung tâm của tứ giác và tách nhau vuông góc.
- Sử dụng lăm le lí loại phụ thân của lối trung trực nhằm minh chứng điều này.
- Nếu tao thấy rằng hai tuyến đường chéo cánh là lối trung trực của nhau, tứ giác này đó là hình thoi.
Cách 3: Hình thoi là tứ giác sở hữu cạnh đều bằng nhau và nhì góc đối đều bằng nhau.
- Sử dụng khái niệm về hình thoi nhằm minh chứng rằng tứ giác sở hữu những cạnh đều bằng nhau và nhì góc đối đều bằng nhau.
- Nếu tao thấy rằng những cạnh của tứ giác đều bằng nhau và nhì góc đối đều bằng nhau, tứ giác này đó là hình thoi.
Đó là phụ thân cơ hội minh chứng một tứ giác là hình thoi. Tùy bám theo đòi hỏi của vấn đề, tao hoàn toàn có thể dùng 1 trong các phụ thân phương pháp này nhằm minh chứng.

_HOOK_
Chứng minh tứ giác là hình thoi tín hiệu nhận ra - Toán lớp 8-P1
Hình thoi: Cùng mày mò những hình thoi tuyệt rất đẹp và phong thái nhập đoạn phim này. Quý khách hàng có khả năng sẽ bị lôi cuốn bởi vì mức độ thú vị của những hình thoi độc đáo và khác biệt và sắc tố tươi tỉnh sáng sủa. Đừng bỏ qua thời cơ mày mò vẻ rất đẹp độc đáo và khác biệt này!
Xem thêm: lời bài hát em gái mưa
Chứng minh tín hiệu nhận ra hình thoi - Toán lớp 8
Dấu hiệu nhận biết: Quý khách hàng là 1 trong những người tinh ma ý và ham muốn mò mẫm hiểu về phong thái nhận ra những tín hiệu quan lại trọng? Hãy coi đoạn phim này nhằm mày mò những tín hiệu nhận ra thú vị và hữu ích tuy nhiên chúng ta trước đó chưa từng biết. Đừng bỏ lỡ thời cơ giao lưu và học hỏi và thưởng thức mới!
Tại sao hình thoi được xem như là một mô hình đặc trưng của tứ giác?
Hình thoi được xem như là một mô hình đặc trưng của tứ giác vì thế nó sở hữu những Điểm sáng và đặc thù riêng lẻ. Dưới đấy là những lí vì thế vì sao hình thoi được xem như là quánh biệt:
1. Cạnh đối tuy nhiên song và bởi vì nhau: Hình thoi sở hữu đối xứng qua quýt lối chéo cánh, tức thị cạnh đối lập cùng nhau tuy nhiên song và đều bằng nhau. Như vậy thực hiện mang đến hình thoi trở thành đặc trưng và dễ dàng nhận ra.
2. Góc đối lập bởi vì nhau: Các góc nhập hình thoi, nhất là những góc đối lập, sở hữu nằm trong kích cỡ. Như vậy Có nghĩa là hình thoi sở hữu những góc đều bằng nhau, canh ty thể hiện nay tính đều và phẳng phiu của hình.
3. Đường chéo cánh tách nhau vuông góc: Đường chéo cánh của hình thoi tách nhau vuông góc bên trên trung điểm của bọn chúng. Đây là 1 trong những điểm đặc trưng và thích mắt khiến cho hình thoi trở thành đặc trưng và lôi cuốn sự lưu ý.
4. Đường trung trực hai tuyến đường chéo: điều đặc biệt của hình thoi là hai tuyến đường chéo cánh của chính nó tách nhau bên trên một điểm và bọn chúng là lối trung trực của nhau. Như vậy Có nghĩa là kể từ điểm tách lối chéo cánh, tao hoàn toàn có thể vẽ hai tuyến đường trực tiếp trung gian ngoan phân chia song những góc của hình thoi.
Tóm lại, hình thoi được xem như là đặc trưng nhập tứ giác vì thế sở hữu cạnh đối tuy nhiên song và đều bằng nhau, góc đối lập đều bằng nhau, lối chéo cánh tách nhau vuông góc và lối trung trực hai tuyến đường chéo cánh. Tính đặc trưng này tạo ra sự rất đẹp và thú vị của hình thoi và nó thông thường được dùng trong tương đối nhiều vấn đề và phần mềm nhập học hành và thực tiễn.
Hình thoi sở hữu tổng số từng nào lối chéo?
Hình thoi sở hữu tổng số 2 lối chéo cánh.
Để minh chứng điều này, tất cả chúng ta hoàn toàn có thể dùng quá trình sau:
Bước 1: Xác lăm le khái niệm của hình thoi. Một hình thoi là 1 trong những tứ giác sở hữu cạnh đối tuy nhiên song và có tính lâu năm đều bằng nhau, những góc đối đều bằng nhau và hai tuyến đường chéo cánh tách nhau vuông góc.
Bước 2: Vẽ hình thoi với hai tuyến đường chéo cánh AC và BD tách nhau bên trên điểm E.
Bước 3: Chứng minh những lối chéo cánh AE và BE tách nhau bên trên điểm M.
Bước 4: Sử dụng những công thức và lăm le lý nhập hình học tập, tất cả chúng ta hoàn toàn có thể minh chứng rằng lối chéo cánh AM và BM không những tách nhau mà còn phải tách nhau vuông góc bên trên điểm M.
Do bại, tất cả chúng ta sở hữu hai tuyến đường chéo cánh nhập hình thoi là AE và BE tách nhau bên trên điểm M, tức là tổng số lối chéo cánh là 2.
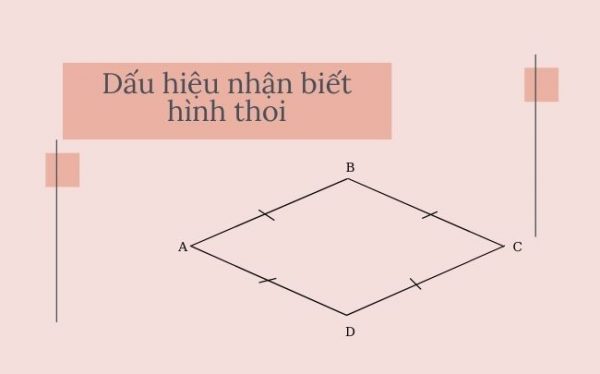
Giả sử sở hữu một tứ giác sở hữu toàn bộ những góc đều bằng nhau, liệu bại sở hữu đầy đủ nhằm minh chứng nó là hình thoi?
Để minh chứng một tứ giác là hình thoi, ko chỉ việc toàn bộ những góc của tứ giác bại đều bằng nhau mà còn phải cần thiết thêm thắt một vài ĐK không giống. Dưới đấy là một vài bước nhằm minh chứng một tứ giác là hình thoi:
Bước 1: Giả sử sở hữu một tứ giác ABCD với toàn bộ những góc là góc đều bằng nhau, tức là ∠A = ∠B = ∠C = ∠D.
Bước 2: Chứng minh tứ giác ABCD là hình bình hành bằng phương pháp minh chứng cả nhì cỗ lối hai tuyến đường đối lập của chính nó là tuy nhiên song và đều bằng nhau.
Bước 3: Sử dụng một trong số cơ hội minh chứng sau nhằm minh chứng tứ giác ABCD là hình thoi:
a) Chứng minh tứ giác ABCD sở hữu tư cạnh bởi vì nhau: AB = BC = CD = DA.
b) Chứng minh tứ giác ABCD sở hữu hai tuyến đường chéo cánh tách nhau vuông góc và chéo cánh tách nhau bên trên trung điểm: Đường chéo cánh AC tách lối chéo cánh BD bên trên trung điểm E và fake sử AE = EC = BE = ED.
c) Chứng minh tứ giác ABCD sở hữu những lối đối tượng người tiêu dùng trải qua trung điểm những cạnh: Đường trung trực của cạnh AB tách lối trung trực của cạnh CD bên trên trung điểm F và fake sử AF = FC. Đường trung trực của cạnh BC tách lối trung trực của cạnh DA bên trên trung điểm G và fake sử BG = GD.
Bước 4: Sau Lúc đang được minh chứng một trong số ĐK bên trên, tao hoàn toàn có thể tóm lại rằng tứ giác ABCD là hình thoi.
Lưu ý rằng quá trình bên trên chỉ là 1 trong những nhập số những cách thức minh chứng một tứ giác là hình thoi. Tuy nhiên, bọn chúng hoàn toàn có thể được dùng nhằm minh chứng trúng một cơ hội tổng quát lác rằng nếu như một tứ giác sở hữu toàn bộ những góc đều bằng nhau và bên cạnh đó vừa lòng những ĐK bổ sung cập nhật, thì bại là 1 trong những hình thoi.
Nếu một tứ giác sở hữu nhì cạnh đối tuy nhiên song và đều bằng nhau, liệu bại sở hữu đầy đủ nhằm minh chứng nó là hình thoi?
Để minh chứng một tứ giác là hình thoi, ko chỉ việc nhì cạnh đối tuy nhiên song và đều bằng nhau mà còn phải cần thiết minh chứng thêm thắt một vài ĐK không giống. Dưới đấy là một phương pháp để hội chứng minh:
Bước 1: Cho một tứ giác sở hữu nhì cạnh đối tuy nhiên song và đều bằng nhau.
Bước 2: Chứng minh rằng cạnh loại phụ thân cũng đều bằng nhau với nhì cạnh đang được biết. Như vậy hoàn toàn có thể được triển khai bằng phương pháp dùng những công thức ĐK tồn bên trên của tứ giác, như lăm le lí tam giác cân nặng, tam giác vuông, hoặc những lăm le lí tương quan cho tới cạnh và góc.
Bước 3: Chứng minh rằng những góc nhập tứ giác đối lập nhau đều bằng nhau. Như vậy hoàn toàn có thể được triển khai bằng phương pháp dùng những lăm le lí về góc đối lập nhập tứ giác, như lăm le lí những góc đối lập nhập tứ giác đều bằng nhau.
Bước 4: Chứng minh rằng hai tuyến đường chéo cánh tách nhau vuông góc cùng nhau. Như vậy hoàn toàn có thể được triển khai bằng phương pháp minh chứng rằng lối chéo cánh khoảng của một tứ giác phân chia tứ giác bại trở thành nhì tam giác cân nặng và những góc tạo nên bởi vì lối chéo cánh với những cạnh là 90 phỏng.
Nếu nhập quy trình minh chứng tứ giác vừa lòng toàn bộ những ĐK bên trên, tao hoàn toàn có thể tóm lại rằng tứ giác này đó là hình thoi.
Chú ý: Đây chỉ là 1 trong những nhập số những cơ hội minh chứng tứ giác là hình thoi. Tùy nhập ĐK và những vấn đề rõ ràng nhập vấn đề, hoàn toàn có thể sở hữu những cơ hội minh chứng không giống nhau.
Xem thêm: tính oxi hóa là gì
Hình thoi sở hữu Điểm sáng gì về góc và cạnh canh ty tất cả chúng ta đơn giản nhận ra nó?
Hình thoi sở hữu những Điểm sáng tại đây canh ty tất cả chúng ta đơn giản nhận ra nó:
1. Cạnh: Hình thoi sở hữu tư cạnh đều đều bằng nhau. Như vậy Có nghĩa là những đoạn trực tiếp nối những đỉnh của hình thoi đều sở hữu phỏng lâu năm như nhau.
2. Góc: Hình thoi sở hữu nhì cặp lối chéo cánh tách nhau bên trên gốc. Như vậy Có nghĩa là những lối chéo cánh của hình thoi phân chia nhỏ tạo hình tư góc đối nhau đều bằng nhau.
Để minh chứng một tứ giác là hình thoi, tất cả chúng ta cũng có thể có một vài cơ hội như sau:
Cách 1: Chứng minh tư cạnh đều bởi vì nhau:
- Sử dụng công thức khoảng cách thân mật nhì điểm nhập hệ tọa phỏng nhằm đo lường và tính toán phỏng lâu năm những cạnh và minh chứng rằng bọn chúng đều bằng nhau.
Cách 2: Chứng minh hai tuyến đường chéo cánh tách nhau bên trên gốc:
- Sử dụng đặc thù lối trung trực của lối chéo cánh nhằm minh chứng rằng hai tuyến đường chéo cánh của tứ giác là lối trung trực của nhau.
Cách 3: Chứng minh tư góc đối bởi vì nhau:
- Sử dụng những luật lệ toán hình học tập như minh chứng nhì góc đối đều bằng nhau, nhì góc cân đối nhau, nhì góc vuông đều bằng nhau nhằm minh chứng rằng tư góc của tứ giác là đều bằng nhau.
Hy vọng những vấn đề bên trên tiếp tục khiến cho bạn nắm rõ rộng lớn về Điểm sáng của hình thoi và cơ hội minh chứng nó.
_HOOK_
Hình thoi - Bài 11 - Toán học tập 8 - Cô Phạm Thị Huệ Chi (Dễ hiểu nhất)
Chứng minh: Tìm hiểu về sự việc minh chứng hoàn toàn có thể thay cho thay đổi cuộc sống thường ngày của bạn! Video này tiếp tục ra mắt cho mình những cơ hội minh chứng hiệu suất cao và mang đến những thành phẩm xứng đáng ngạc nhiên. Đừng bỏ qua thời cơ được chuẩn bị kiến thức và kỹ năng mới mẻ và sở hữu sự thay cho thay đổi tích vô cùng nhập cuộc sống thường ngày của bạn!











Bình luận