Công thức tính đường cao trong tam giác thường, cân, đều, vuông

Đường cao vô tam giác là một trong đường thẳng liền mạch với đặc điểm cần thiết và tương quan thật nhiều cho tới những vấn đề hình học tập phẳng lặng. Vậy lối cao là gì, phương pháp tính lối cao vô tam giác ra sao. Cùng xem thêm nội dung bài viết sau đây để sở hữu câu vấn đáp và biết công thức tính lối cao vô tam giác giản dị nhất nhé.

Công thức tính lối cao vô tam giác

Tính lối cao vô tam giác thường

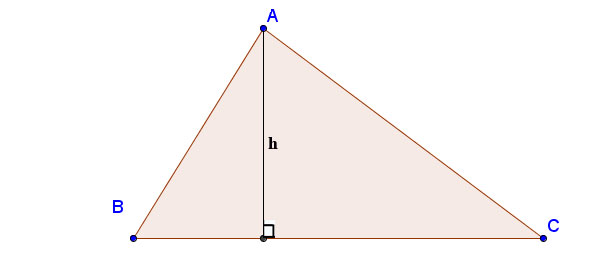
Bạn đang xem: đường cao tam giác vuông

Cách tính lối cao vô tam giác dùng công thức Heron:

$h_a=2 \frac{\sqrt{p(p-a)(p-b)(p-c)}}{a}$

Với a, b, c là phỏng lâu năm những cạnh; ha là lối cao được kẻ kể từ đỉnh A xuống cạnh BC; p là nửa chu vi:

$p=\frac{(a+b+c)}{2}$

Ví dụ:

Cho tam giác ABC, cạnh AB = 4 centimet, cạnh BC = 7 centimet, cạnh AC = 5 centimet. Tính lối cao AH Tính từ lúc A hạn chế BC bên trên H và tính diện tích S ABC.

Giải:

Nửa chu vi tam giác: Phường = (AB + BC + AC) : 2 = (4 + 7 + 5) : 2 = 8(cm)

Chiều cao $AH=2 \frac{\sqrt{p(p-A B)(p-A C)(p-B C)}}{A B}$ $=2 \frac{\sqrt{8(8-4)(8-5)(8-7)}}{4}$

=> $AH = 4 \sqrt{8}(cm)$

Xét tam giác ABC, tao có:

$S_{A B C}=\frac{1}{2} \mathrm{AH} \cdot \mathrm{BC}=\frac{1}{2} 4 \sqrt{8} \times 7=14 \sqrt{8}\left(cm^2\right)$

Như vậy, $\mathrm{AH}=4 \sqrt{8}(cm), S_{A B C}=14 \sqrt{8}\left(cm^2\right)$

Tính lối cao vô tam giác đều

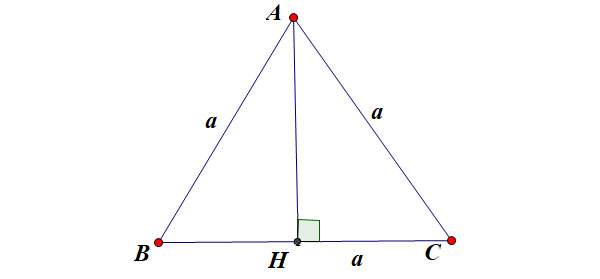
Giả sử tam giác đều ABC có tính lâu năm cạnh vị a như hình vẽ:

$h=a \frac{\sqrt{3}}{2}$

Trong đó:

h là lối cao của tam giác đều
a là phỏng lâu năm cạnh của tam giác đều

Công thức tính lối cao vô tam giác vuông

Tam giác vuông

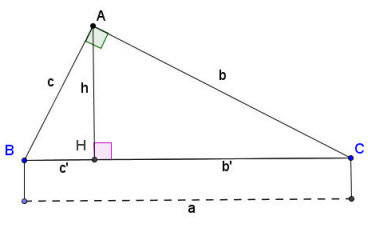
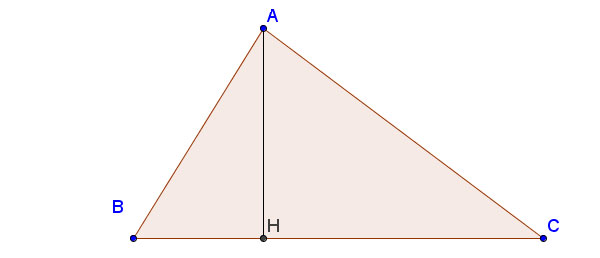
Giả sử với tam giác vuông ABC vuông bên trên A như hình vẽ trên:

Công thức tính cạnh và lối cao vô tam giác vuông:

1. a²= b²+ c²

2. b²= a.b′ và c²= a.c′

3. a.h = b.c

4. h²= b′.c'

5. $\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}$

Trong đó:

a, b, c theo lần lượt là những cạnh của tam giác vuông như hình trên;
b’ là lối chiếu của cạnh b bên trên cạnh huyền;
c’ là lối chiếu của cạnh c bên trên cạnh huyền;
h là độ cao của tam giác vuông được kẻ kể từ đỉnh góc vuông A xuống cạnh huyền BC.

Ví dụ 1: Cho tam giác ABC vuông bên trên A, lối cao AH. Tính BC, AC, AH biết AB = 15cm, HC = 16cm.

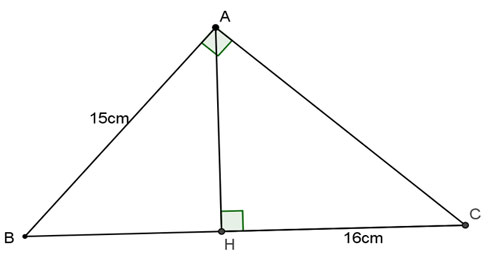
Cho tam giác ABC vuông bên trên A, lối cao AH

Giải:

Áp dụng hệ thức lượng vô tam giác vuông ABC có:

AC² = CH.BC = 16.BC

Theo tấp tểnh lí Pythagore mang đến tam giác ABC vuông gại A tao có:

AB² + AC² = BC²

⇔ 15² + 16.BC = BC²

⇔ BC² - 16.BC - 225 = 0

⇔ BC² - 25.BC + 9.BC - 225 = 0

⇔ BC(BC - 25) + 9(BC - 25) = 0

⇔ (BC - 25)(BC + 9) = 0

⇔ BC = 25 hoặc BC = -9 (loại)

⇒ AC² = 16.BC = 16.25 = 400 ⇒ AC = trăng tròn (cm)

Xem thêm: tính chu vi đường tròn

Xét tam giác vuông ABC có: AH.BC = AB.AC (hệ thức lượng)

=> AH = AB.AC/BC = 15.20/25 = 12(cm)

Vậy BC=25(cm); AC=20(cm); AH=12(cm)

Ví dụ 2:

Cho tam giác ABC vuông bên trên A, AB=24cm, AC=32cm. Đường trung trực của BC hạn chế AC, BC theo đòi trật tự D và E. Tính DE.

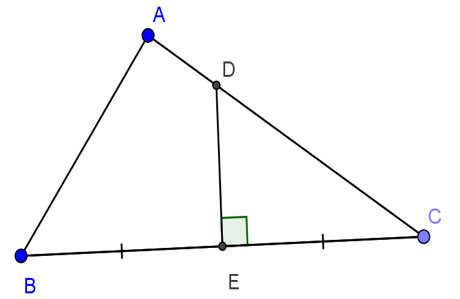
Cho tam giác ABC vuông bên trên A

Giải:

Xét tam giác vuông ABC, tao có:

BC² = AB²+ AC² ( theo đòi tấp tểnh lý py-ta-go)

BC² = 24²+ 32²

BC² = 1600

BC = 40(cm)

EC = BC : 2 = 40 : 2 = 20(cm)

Xét tam giác vuông Ngân Hàng Á Châu và tam giác vuông ECD có:

Có ∠A = ∠E = 90o

∠C chung

=> Tam giác Ngân Hàng Á Châu ∾ tam giác ECD (g.g)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

Vậy ED = 15cm

Công thức tính lối cao vô tam giác cân

Tam giác cân

Giả sử chúng ta với tam giác ABC cân nặng bên trên A, lối cao AH vuông góc bên trên H như hình trên:

Công thức tính lối cao AH:

Vì tam giác ABC cân nặng bên trên A nên lối cao AH mặt khác là lối trung tuyến nên:

⇒ HB=HC= ½BC

Áp dụng tấp tểnh lý Pytago vô tam giác vuông ABH vuông bên trên H tao có:

AH²+BH²=AB²

⇒AH²=AB²−BH²

Ví dụ: Cho Δ ABC cân nặng bên trên A với BC = 30(cm), lối cao AH = 20(cm). Tính lối cao ứng với cạnh mặt mày của tam giác cân nặng cơ.

Giải: Xét Δ ABC cân nặng bên trên A với BC = 30(cm)

⇒ BH = CH = 15(cm).

Áp dụng đinh lý Py – tao – go tao có:

$AB=\sqrt{\left(AH^2+HB^2\right)}$ $=\sqrt{\left(20^2+15^2\right)} =25 cm$

Kẻ $\mathrm{BK} \perp \mathrm{AC}$ , giờ tao nên tính BK = ?

Ta có: $\mathrm{S}_{\mathrm{ABC}}=\frac{1}{2} \cdot\mathrm{AH} \cdot \mathrm{BC}$ $=\frac{1}{2}.20.30\ =\ 300 (cm^{2})$

Mặt không giống $\mathrm{S}_{\mathrm{ABC}}=\frac{1}{2} \cdot \mathrm{BK} \cdot \mathrm{AC}=\frac{1}{2} \cdot \mathrm{BK} \cdot 25$

Do cơ, tao với $\frac{1}{2}.BK.25 = 300$ ⇔ $BK=\frac{2.300}{25}=24(cm)$

Định nghĩa lối cao vô tam giác

Đường cao vô tam giác là đoạn vuông góc kẻ từ là 1 đỉnh cho tới cạnh đối lập. Cạnh đối lập này được gọi là lòng ứng với lối cao. Độ lâu năm của lối cao là khoảng cách đằm thắm đỉnh và lòng.

Xem thêm: Xôi Lạc TV: Cập nhật tỷ lệ kèo nhà cái mới nhất nhanh nhất

Đường cao vô tam giác

Tính hóa học tía lối cao của một tam giác

Ba lối cao của tam giác nằm trong trải qua một điểm. Điểm cơ gọi là trực tâm của tam giác.

Các các bạn chỉ việc tính những bộ phận chưa chắc chắn trong những công thức tính lối cao vô tam giác phía trên là hoàn toàn có thể tính được lối cao vô tam giác.