Tìm m nhằm hàm số không có cực trị (hàm số bậc 3) với điều giải nhằm chúng ta xem thêm.
KHÓA ÔN CHUYÊN ĐỀ THI TỐT NGHIỆP THPT
Bạn đang xem: hàm số không có cực trị
NHANH CHÓNG LẤP LỖ HỔNG KIẾN THỨC - TỰ TIN NHẬP CUỘC ĐƯỜNG ĐUA ĐẠI HỌC
✅ Hệ thống hóa kỹ năng và kiến thức trọng tâm theo đòi từng mục chính đua chất lượng nghiệp THPT
✅ Cung cấp cho những cách thức thực hiện bài xích hiệu suất cao theo đòi từng chuyên nghiệp đề THPT
✅ Lưu ý những lỗi sai thông thường bắt gặp và tips, mẹo tăng thêm vận tốc thực hiện bài
✅ Đầy đầy đủ những môn Toán - Lí - Hóa - Anh - Văn - Sinh - Sử - Địa - GDCD
✅ Học phí chỉ 50K/chuyên đề

Tham khảo thêm:
- Cực trị của hàm số
- Tìm m nhằm hàm số với 7 đặc biệt trị
- Tìm m nhằm hàm số với 3 đặc biệt trị
Xét hàm số sau: hắn = ax3 + bx2 + cx + d với a ≠ 0
Khi tê liệt y’ = 3ax2 + 2bx+c với y’ = 0 ⇔ 3ax2 + 2bx+c=0
Hàm số không tồn tại đặc biệt trị Lúc và chỉ Lúc phương trình y’ = 0 vô nghiệm hoặc là với nghiệm kép ⇔ Δ’ ≤ 0 ⇔ b2-3ac ≤ 0
Tìm m nhằm hàm số không có cực trị – Bài tập
Tìm m nhằm hàm số không có cực trị (ví dụ 1)
Tìm tổng số độ quý hiếm nguyên vẹn của m nhằm hàm số
![]() không với đặc biệt trị:
không với đặc biệt trị:
- A. 5
- B. 3
- C. 4
- D. 7
Lời giải chi tiết
Đáp án đúng: A
Ta với y’ = x2 + 2mx – (2m – 3)
Xét y’ = 0 ⇔ x2 + 2mx – (2m – 3) = 0
Hàm số vẫn không tồn tại đặc biệt trị Lúc vài ba chỉ Lúc y’ = 0 với tối nhiều 1 nghiệm
Xem thêm: lời bài hát em gái mưa
⇔ Δ’ ≤ 0 ⇔ m2 + (2m – 3) ≤ 0 ⇔ -3 ≤m≤ 1
Kết phù hợp với ĐK m nguyên vẹn nên m{-3;-2;-1;0;1}
Vậy sẽ có được 5 độ quý hiếm m thỏa mãn nhu cầu đòi hỏi câu hỏi.
Tìm m nhằm hàm số không có cực trị (ví dụ 2)
Với độ quý hiếm này của thông số m thì hàm số hắn = x3 – 3x2 + 3(1 – m2)x + 1 tiếp tục không tồn tại đặc biệt trị.
- A. m ≠ 2
- B. m ∈ R
- C. m = 0
- D. Không tồn bên trên m
Lời giải chi tiết
Đáp án đúng: C
Ta với y’ = 3x2 – 6x + 3(1 – m2) với y’ = 0 ⇔ x2-2x + 1 – m2 = 0
Hàm số vẫn mang đến tiếp tục không tồn tại điểm đặc biệt trị Lúc phương trình y’ = 0 vô nghiệm hoặc với nghiệm kép ⇔ Δ’ ≤ 0 ⇔ 1 – (1 – m2) ≤ 0 ⇔ m2 ≤ 0 vậy m=0 thỏa mã đòi hỏi câu hỏi.
Tìm m nhằm hàm số không có cực trị (ví dụ 3)
Cho hàm số sau: hắn = -2x3+(2m – 1)x2-(m2 – 1)x – 2. Tìm toàn bộ những độ quý hiếm của thông số m nhằm hàm số vẫn mang đến tiếp tục không tồn tại đặc biệt trị .
Lời giải chi tiết
Chúng tớ với y’ = -6x2 + 2(2m – 1)x – (m2 – 1) với y’ = 0 ⇔ -6x2 + 2(2m – 1)x – (m2 – 1) = 0
Hàm số vẫn mang đến tiếp tục không tồn tại đặc biệt trị Lúc phương trình y’ = 0 với vô nghiệm hoặc là với nghiệm kép

Tìm m nhằm hàm số không có cực trị (ví dụ 4)
Tìm toàn bộ những độ quý hiếm của thông số m nhằm hàm số ![]() sẽ không tồn tại đặc biệt trị.
sẽ không tồn tại đặc biệt trị.
Lời giải chi tiết
– Với tình huống m=1 hàm số vẫn mang đến tiếp tục phát triển thành hắn = 3x2 + x + 2 đấy là hàm số bậc nhị nên luôn luôn chỉ mất có một không hai 1 đặc biệt trị.
→ Vậy với m=1 (loại)
– Trường phù hợp m ≠ 1, với y’ = (m – 1)x2 + 2(m + 2)x + m với y’ = 0 ⇔ (m – 1)x2 + 2(m + 2)x + m = 0
Xem thêm: đại học hàng hải điểm chuẩn
Hàm số vẫn mang đến tiếp tục không tồn tại đặc biệt trị Lúc phương trình y’ = 0 vô nghiệm hoặc là với nghiệm kép
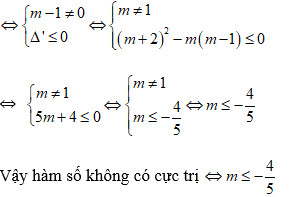
Trên đấy là một trong những bài xích tập Tìm m nhằm hàm số không có cực trị với điều giải (toán 12) nhằm chúng ta xem thêm.











Bình luận