phương trình bậc 2 1 ẩn

Phương trình bậc 2 một ẩn là 1 trong trong mỗi kỹ năng và kiến thức cần thiết nhập công tác toán trung học tập hạ tầng. Vì vậy, thời điểm ngày hôm nay Kiến Guru van ra mắt cho tới độc giả nội dung bài viết về chủ thể này. Bài viết lách tiếp tục tổ hợp những lý thuyết căn bạn dạng, bên cạnh đó cũng thể hiện những dạng toán thông thường bắt gặp và những ví dụ vận dụng một cơ hội cụ thể, rõ rệt. Đây là chủ thể yêu thích, hoặc xuất hiện tại ở những đề đua tuyển chọn sinh. Cùng Kiến Guru tò mò nhé:

Bạn đang xem: phương trình bậc 2 1 ẩn

Phương trình bậc 2 một ẩn là gì?

Cho phương trình sau: ax²+bx+c=0 (a≠0), được gọi là phương trình bậc 2 với ẩn là x.

Công thức nghiệm: Ta gọi Δ=b²-4ac.Khi đó:

• Δ>0: phương trình tồn bên trên 2 nghiệm:.

• Δ=0, phương trình với nghiệm kép x=-b/2a
• Δ<0, phương trình đang được mang lại vô nghiệm.

Trong tình huống b=2b’, nhằm giản dị tao rất có thể tính Δ’=b’²-ac, tương tự động như trên:

• Δ’>0: phương trình với 2 nghiệm phân biệt.

• Δ’=0: phương trình với nghiệm kép x=-b’/a
• Δ’<0: phương trình vô nghiệm.

Định lý Viet và phần mềm nhập phương trình bậc 2 một ẩn.

Cho phương trình bậc 2 một ẩn: ax²+bx+c=0 (a≠0). Giả sử phương trình với 2 nghiệm x₁ và x₂, thời điểm hiện tại hệ thức sau được thỏa mãn:

Dựa nhập hệ thức vừa vặn nêu, tao rất có thể dùng lăm le lý Viet nhằm tính những biểu thức đối xứng chứa chấp x₁ và x₂

• x₁+x₂=-b/a
• x₁²+x₂²=(x₁+x₂)²-2x₁x₂=(b²-2ac)/a²
• 
• …

Nhận xét: Đối với dạng này, tao cần thiết thay đổi biểu thức làm thế nào cho xuất hiện tại (x₁+x₂) và x₁x₂ nhằm vận dụng hệ thức Viet.

Định lý Viet đảo: Giả sử tồn bên trên nhị số thực x₁ và x₂ thỏa mãn: x₁+x₂=S, x₁x₂=P thì x₁ và x₂ là 2 nghiệm của phương trình x²-Sx+P=0

Một số phần mềm thông thường bắt gặp của lăm le lý Viet nhập giải bài bác tập luyện toán:

• Nhẩm nghiệm phương trình bậc 2: mang lại phương trình ax²+bx+c=0 (a≠0), 
• Nếu a+b+c=0 thì phương trình với nghiệm x₁=1 và x₂=c/a
• Nếu a-b+c=0 thì phương trình với nghiệm x₁=-1 và x₂=-c/a

• Phân tích nhiều thức trở thành nhân tử: mang lại nhiều thức P(x)=ax²+bx+c nếu như x₁ và x₂ là nghiệm của phương trình P(x)=0 thì nhiều thức P(x)=a(x-x₁)(x-x₂)
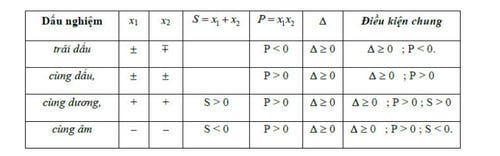
• Xác lăm le lốt của những nghiệm: mang lại phương trình ax²+bx+c=0 (a≠0), fake sử x₁ và x₂ là 2 nghiệm của phương trình. Theo lăm le lý Viet, tao có:

• Nếu S<0, x1 và x₂ trái ngược lốt.
• Nếu S>0, x₁ và x₂ nằm trong dấu:
• P>0, nhị nghiệm nằm trong dương.
• P<0, nhị nghiệm đồng âm.

II. Dạng bài bác tập luyện về phương trình bậc 2 một ẩn:

Dạng 1: Bài tập luyện phương trình bậc 2 một ẩn ko xuất hiện tại thông số.

Để giải những phương trình bậc 2, cơ hội phổ cập nhất là dùng công thức tính Δ hoặc Δ’, rồi vận dụng những ĐK và công thức của nghiệm và đã được nêu ở mục I.

Ví dụ 1: Giải những phương trình sau:

1. x²-3x+2=0
2. x²+x-6=0

Hướng dẫn:

1. Δ=(-3)²-4.2=1. Vậy

Ngoài đi ra, tao rất có thể vận dụng phương pháp tính nhanh: nhằm ý

suy đi ra phương trình với nghiệm là x₁=1 và x₂=2/1=2

1. Δ=1²-4.(-6)=25. Vậy

Tuy nhiên, ngoài các phương trình bậc 2 không thiếu, tao cũng xét những tình huống quan trọng đặc biệt sau:

Phương trình khuyết hạng tử.

Khuyết hạng tử bậc nhất: ax²+c=0 (1).

Phương pháp:

• 
• Nếu -c/a>0, nghiệm là:

• Nếu -c/a=0, nghiệm x=0
• Nếu -c/a<0, phương trình vô nghiệm.

Khuyết hạng tử tự động do: ax²+bx=0 (2). Phương pháp:

Ví dụ 2:  Giải phương trình:

1. x²-4=0
2. x²-3x=0

Hướng dẫn:

1. x²-4=0 ⇔ x²=4 ⇔ x=2 hoặc x=-2
2. x²-3x=0 ⇔ x(x-3)=0 ⇔ x=0 hoặc x=3

Phương trình đem về dạng bậc 2.

Phương trình trùng phương: ax⁴+bx²+c=0 (a≠0):

Xem thêm: viết bài văn tả cảnh sinh hoạt

• Đặt t=x² (t≥0).
• Phương trình đang được mang lại về dạng: at²+bt+c=0
• Giải như phương trình bậc 2 thông thường, lưu ý ĐK t≥0

Phương trình chứa chấp ẩn ở mẫu:

• Tìm ĐK xác lập của phương trình (điều khiếu nại nhằm hình mẫu số không giống 0).
• Quy đồng khử hình mẫu.
• Giải phương trình vừa vặn cảm nhận được, lưu ý đối chiếu với ĐK ban sơ.

Chú ý: phương pháp đặt  t=x² (t≥0) được gọi là cách thức đặt điều ẩn phụ. Ngoài đặt điều ẩn phụ như bên trên, so với một vài câu hỏi, cần thiết khôn khéo lựa lựa chọn sao mang lại ẩn phụ là tốt nhất có thể nhằm mục tiêu đem câu hỏi kể từ bậc cao về dạng bậc 2 không xa lạ. Ví dụ, rất có thể đặt điều t=x+1, t=x²+x, t=x²-1…

Ví dụ 3: Giải những phương trình sau:

1. 4x⁴-3x²-1=0
2. 

Hướng dẫn:

1. Đặt t=x² (t≥0), thời điểm hiện tại phương trình trở thành:

4t²-3t-1=0, suy đi ra t=1 hoặc t=-¼

• t=1 ⇔ x²=1  ⇔ x=1 hoặc x=-1.
• t=-¼ , loại vì thế ĐK t≥0

Vậy phương trình với nghiệm x=1 hoặc x=-1.

1. Ta có:

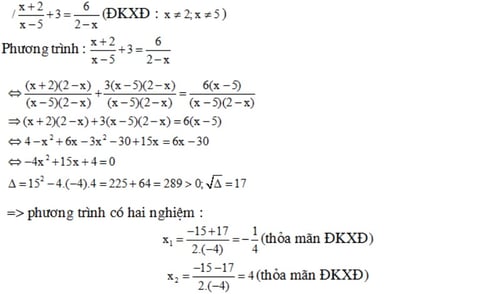
Dạng 2: Phương trình bậc 2 một ẩn với thông số.

Biện luận số nghiệm của phương trình bậc 2.

Phương pháp: Sử dụng công thức tính Δ, nhờ vào lốt của Δ nhằm biện luận phương trình với 2 nghiệm phân biệt, với nghiệm kép hoặc là vô nghiệm.

Ví dụ 4: Giải và biện luận theo gót thông số m: mx²-5x-m-5=0 (*)

Hướng dẫn:

Xét m=0, Khi bại (*) ⇔ -5x-5=0 ⇔ x=-1

Xét m≠0, Khi bại (*) là phương trình bậc 2 theo gót ẩn x.

• 
• Vì Δ≥0 nên phương trình luôn luôn với nghiệm:
• Δ=0  ⇔ m=-5/2, phương trình với nghiệm có một không hai.
• Δ>0 ⇔ m≠-5/2, phương trình với 2 nghiệm phân biệt:

Xác lăm le ĐK thông số nhằm nghiệm thỏa đòi hỏi đề bài bác.

Phương pháp: nhằm nghiệm thỏa đòi hỏi đề bài bác, trước tiên phương trình bậc 2 cần với nghiệm. Vì vậy, tao triển khai theo gót công việc sau:

• Tính Δ, lần ĐK nhằm Δ ko âm.
• Dựa nhập lăm le lý Viet, tao giành được những hệ thức thân thiện tích và tổng, kể từ bại biện luận theo gót đòi hỏi đề.

Ví dụ 5: Cho phương trình x2+mx+m+3=0 (*). Tìm m nhằm phương trình (*) với 2 nghiệm thỏa mãn:

Hướng dẫn:

Để phương trình (*) với nghiệm thì:

Khi bại, gọi x₁ và x₂ là 2 nghiệm, theo gót lăm le lý Viet:

Mặt khác:

Theo đề:

Xem thêm: luyện từ và câu lớp 3

Thử lại:

• Khi m=5, Δ=-7 <0 (loại)
• Khi m=-3, Δ=9 >0 (nhận)

vậy m = -3 thỏa đòi hỏi đề bài bác.

Trên đó là tổ hợp của Kiến Guru về phương trình bậc 2 một ẩn. Hy vọng qua quýt nội dung bài viết, những các bạn sẽ nắm rõ rộng lớn về chủ thể này. Ngoài việc tự động gia tăng kỹ năng và kiến thức mang lại bạn dạng thân thiện, chúng ta cũng tiếp tục tập luyện thêm thắt được trí tuệ giải quyết và xử lý những câu hỏi về phương trình bậc 2. Các các bạn cũng rất có thể tìm hiểu thêm thêm thắt những nội dung bài viết không giống bên trên trang của Kiến Guru nhằm tò mò thêm thắt nhiều kỹ năng và kiến thức mới mẻ. Chúc chúng ta sức mạnh và tiếp thu kiến thức tốt!