số điểm cực trị của hàm số

Lý thuyết cực kỳ trị của hàm số

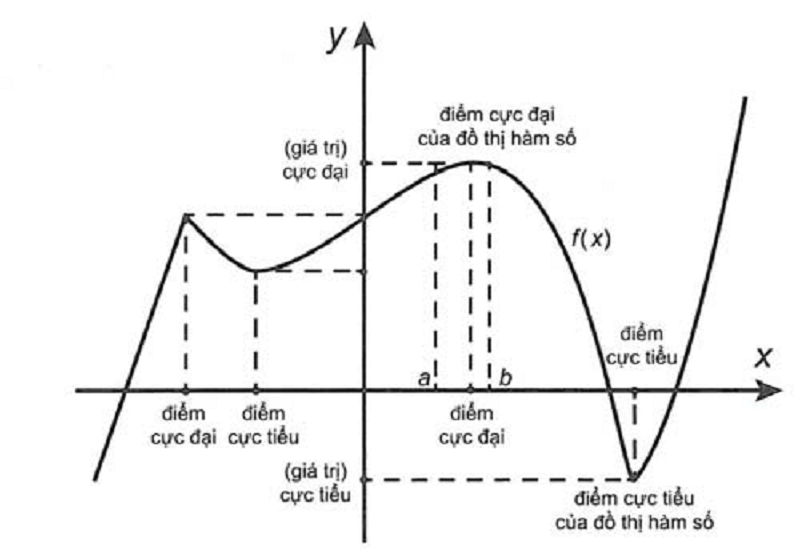
Cực trị của hàm số là vấn đề có mức giá trị lớn số 1 hoặc nhỏ nhất đối với xung xung quanh tuy nhiên hàm số hoàn toàn có thể đạt được. Trong hình học tập, nó biểu biểu diễn khoảng cách lớn số 1 hoặc nhỏ nhất kể từ đặc điểm này thanh lịch điểm kia. 

Bạn đang xem: số điểm cực trị của hàm số

1. Định nghĩa

Giả sử hàm số f xác lập bên trên K (K ⊂ ℝ) và x0 ∈ K.

• x0 được gọi là vấn đề cực lớn của hàm số f nếu như tồn bên trên một khoảng tầm (a;b) ⊂ K chứa chấp điểm x0 sao mang lại f(x) < f(x0), ∀ x ∈ (a;b) \{x0}. Khi cơ f(x0) được gọi là giá trị cực kỳ đại của hàm số f.

• x0 được gọi là vấn đề cực kỳ tè của hàm số f nếu như tồn bên trên một khoảng tầm (a;b) ⊂ K chứa chấp điểm x0 sao mang lại f(x) > f(x0), ∀ x ∈ (a;b) \{x0}. Khi cơ f(x0) được gọi là giá trị cực kỳ tiểu của hàm số f.

Một số Note chung:

1. Điểm cực lớn (cực tiểu) x0 được gọi công cộng là vấn đề cực kỳ trị. Giá trị cực lớn (cực tiểu) f(x0) của hàm số được gọi công cộng là cực kỳ trị. Hàm số hoàn toàn có thể đạt cực lớn hoặc cực kỳ tè trên rất nhiều điểm bên trên hội tụ K.

2. Nói công cộng, độ quý hiếm cực lớn (cực tiểu) f(x0) ko nên là độ quý hiếm lớn số 1 (nhỏ nhất) của hàm số f bên trên luyện K; f(x0) đơn thuần độ quý hiếm lớn số 1 (nhỏ nhất) của hàm số f bên trên một khoảng tầm (a;b) chứa chấp x0.

3. Nếu x0 là 1 trong điểm cực kỳ trị của hàm số f thì điểm (x0; f(x0)) được gọi là vấn đề cực kỳ trị của vật dụng thị hàm số f.

2. Điều khiếu nại cần thiết và đầy đủ nhằm hàm số đạt cực kỳ trị

Hàm số đem cực kỳ trị khi nào? Để một hàm số hoàn toàn có thể đạt cực kỳ trị bên trên một điểm thì hàm số cần thiết vừa lòng những nguyên tố sau (bao gồm: ĐK cần thiết và ĐK đủ).

Điều khiếu nại cần

Định lý 1: Giả sử hàm số f đạt cực kỳ trị bên trên điểm x0. Khi cơ, nếu như f đem đạo hàm bên trên điểm x0 thì f’(x0) = 0.

Một số Note chung:

1. Điều ngược lại hoàn toàn có thể ko đích. Đạo hàm f’ hoàn toàn có thể vày 0 bên trên điểm x0 tuy nhiên hàm số f ko đạt cực kỳ trị bên trên điểm x0.

2. Hàm số hoàn toàn có thể đạt cực kỳ trị bên trên một điểm tuy nhiên bên trên cơ hàm số không tồn tại đạo hàm.

Điều khiếu nại đủ

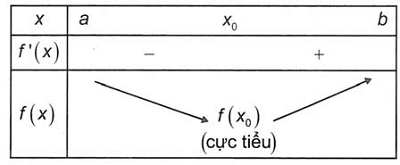
Định lý 2: Nếu f’(x) thay đổi lốt kể từ âm thanh lịch dương khi x trải qua điểm x0 (theo chiều tăng) thì hàm số đạt cực kỳ tè bên trên x0.

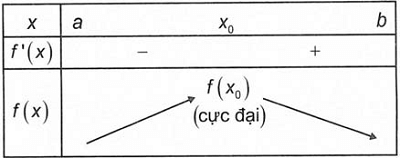
Nếu f’(x) thay đổi lốt kể từ dương thanh lịch âm khi x trải qua điểm x0 (theo chiều tăng) thì hàm số đạt cực lớn bên trên x0.

Định lý 3: Giả sử hàm số f đem đạo hàm cung cấp một bên trên khoảng tầm (a;b) chứa chấp điểm x0, f’(x0) = 0 và f đem đạo hàm cung cấp nhì không giống 0 bên trên điểm x0.

• Nếu f’’(x0) < 0 thì hàm số f đạt cực lớn bên trên điểm x0.

• Nếu f’’(x0) > 0 thì hàm số f đạt cực kỳ tè bên trên điểm x0.

• Nếu f’’(x0) = 0 thì tao ko thể Tóm lại được, cần thiết lập bảng trở nên thiên hoặc bảng xét lốt đạo hàm.

Hướng dẫn cơ hội thăm dò cực kỳ trị của một trong những hàm số thông thường gặp

Mỗi hàm số đều phải có một đặc thù và cơ hội thăm dò cực kỳ trị không giống nhau. Ngay tại đây Monkey tiếp tục reviews cho tới các bạn phương pháp tính cực kỳ trị của hàm số thông thường bắt gặp trong những đề đua nhất.

Cực trị của hàm số bậc 2

Hàm số bậc 2 đem dạng: y = ax2 + bx + c (a ≠ 0) với miền xác lập là D = R. Ta có: y’ = 2ax + b.

• y’ thay đổi lốt khi x qua chuyện x0 = -b/2a

• Hàm số đạt cực kỳ trị bên trên x0 = -b/2a

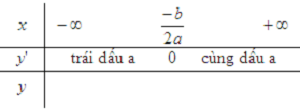
Cực trị của hàm số bậc 3

Hàm số bậc 3 đem dạng: y = ax3 + bx2 + cx + d (a ≠ 0) với miền xác lập là D = R. Ta có: y’ = 3ax2 + 2bx + c → Δ’ = b2 – 3ac.

• Δ’ ≤ 0 : y’ ko thay đổi lốt → hàm số không tồn tại cực kỳ trị

• Δ’ > 0 : y’ thay đổi lốt gấp đôi → hàm số đem nhì cực kỳ trị (1 CĐ và 1 CT)

Cách thăm dò đường thẳng liền mạch trải qua nhì cực kỳ trị của hàm số bậc ba:

Ta hoàn toàn có thể phân tách : y = f(x) = (Ax + B)f ‘(x) + Cx + D bằng phương pháp phân tách nhiều thức f(x) mang lại nhiều thức f ‘(x).

Giả sử hàm số đạt cực kỳ trị bên trên x1 và x2

Ta có: f(x1) = (Ax1 + B)f ‘(x1) + Cx1 + D → f(x1) = Cx1 + D vì như thế f ‘(x1) = 0

Tương tự: f(x2) = Cx2 + D vì như thế f ‘(x2) = 0

Kết luận: Đường trực tiếp qua chuyện nhì điểm cực kỳ trị đem phương trình: nó = Cx + D

Cực trị của hàm số bậc 4 (Hàm trùng phương)

Hàm số trùng phương đem dạng: y = ax4 + bx2 + c (a ≠ 0) với miền xác lập là D = R. Ta có: y’ = 4ax^3 + 2bx = 2x(2ax^2 + b) và y’ = 0 x = 0 2ax^2 + b = 0 x = 0 x62 = -b/2a.

• Khi -b/2a $\le$ 0 <=> b/2a $\ge$ 0 thì y’ chỉ thay đổi lốt 1 phen khi x trải qua x0 = 0 → Hàm số đạt cực kỳ trị bên trên xo = 0

• Khi -b/2a > 0 <=> b/2a < 0 thì y’ thay đổi lốt 3 phen → hàm số đem 3 cực kỳ trị

Cực trị của hàm con số giác

Phương pháp thăm dò cực kỳ trị của hàm con số giác như sau:

• Bước 1: Tìm miền xác lập của hàm số.

• Bước 2: Tính đạo hàm y’ = f’(x), giải phương trình y’=0, fake sử đem nghiệm x=x0.

• Bước 3: Khi cơ tao thăm dò đạo hàm y’’. 

• Tính y’’(x0) rồi thể hiện Tóm lại nhờ vào quyết định lý 2.

Cực trị của hàm số logarit

Chúng tao rất cần được tiến hành theo đòi quá trình sau:

• Bước 1: Tìm miền xác lập của hàm số.

• Bước 2: Tính đạo hàm y’, rồi giải phương trình  y’=0, fake sử đem nghiệm x=x0.

  Xem thêm: đạo hàm của căn x

• Bước 3: Xét nhì khả năng:

  • Tìm đạo hàm y’’.

  • Tính y’’(x0) rồi thể hiện Tóm lại nhờ vào quyết định lý 3.

• Nếu xét được lốt của y’: Khi đó: lập bảng trở nên thiên rồi thể hiện Tóm lại nhờ vào quyết định lý 2.

• Nếu ko xét được lốt của y’: Khi đó:

Các dạng bài bác luyện áp dụng thông thường gặp

Vì những vấn đề về cực kỳ trị xuất hiện tại thông thường xuyên trong những đề đua trung học phổ thông Quốc Gia từng năm. Nắm bắt được tình hình công cộng, Monkey đang được tổ hợp 3 dạng vấn đề thông thường bắt gặp tương quan cho tới cực kỳ trị của hàm số, canh ty chúng ta cũng có thể dễ dàng và đơn giản ôn luyện rộng lớn.

Dạng 1: Tìm điểm cực kỳ trị của hàm số

Có 2 phương thức nhằm giải dạng vấn đề thăm dò số điểm cực trị của hàm số, chúng ta cũng có thể theo đòi dõi tức thì sau đây.

Cách 1:

• Bước 1: Tìm luyện xác lập của hàm số.

• Bước 2: Tính f'(x). Tìm những điểm bên trên cơ f'(x)bằng 0 hoặc f'(x) ko xác lập.

• Bước 3: Lập bảng trở nên thiên.

• Bước 4: Từ bảng trở nên thiên suy đi ra những điểm cực kỳ trị.

Cách 2:

• Bước 1: Tìm luyện xác lập của hàm số.

• Bước 2: Tính f'(x). Giải phương trình f'(x)và ký hiệu xi (i=1,2,3,...)là những nghiệm của chính nó.

• Bước 3: Tính f''(x) và f''(xi ) .

• Bước 4: Dựa vô lốt của f''(xi )suy đi ra đặc thù cực kỳ trị của điểm xi.

Ví dụ:

Tìm cực kỳ trị của hàm số nó = 2x3 - 6x + 2.

Hướng dẫn giải:

Tập xác lập D = R.

Tính y' = 6x^2 - 6. Cho y'= 0 ⇔ 6x2 - 6 = 0 ⇔ x = ±1.

Bảng trở nên thiên:

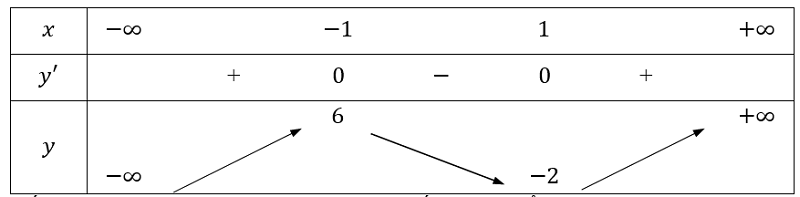
Vậy hàm số đạt cực lớn bên trên x = - 1, nó = 6 và hàm số đạt cực kỳ tè bên trên x = 1,nó = -2.

Dạng 2: Tìm thông số m nhằm hàm số đạt cực kỳ trị bên trên một điểm

Phương pháp giải:

Trong dạng toán này tao chỉ xét tình huống hàm số đem đạo hàm bên trên x0. Khi cơ nhằm giải vấn đề này, tao tổ chức theo đòi nhì bước.

• Bước 1: Điều khiếu nại cần thiết nhằm hàm số đạt cực kỳ trị bên trên x0 là y'(x0) = 0, kể từ ĐK này tao tìm ra độ quý hiếm của thông số .

• Bước 2: Kiểm lại bằng phương pháp người sử dụng một trong các nhì quy tắc thăm dò cực kỳ trị ,nhằm xét coi độ quý hiếm của thông số một vừa hai phải tìm ra đem vừa lòng đòi hỏi của vấn đề hoặc không?

Ví dụ:

Cho hàm số nó = x^3 - 3mx^2 +(m^2 - 1)x + 2, m là thông số thực. Tìm toàn bộ những độ quý hiếm của m nhằm hàm số đang được mang lại đạt cực kỳ tè bên trên x = 2.

Hướng dẫn giải:

Tập xác lập D = R. Tính y'=3x^2 - 6mx + m^2 - 1; y'' = 6x - 6m.

Hàm số đang được mang lại đạt cực kỳ tè bên trên x = 2 → 

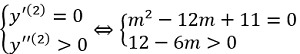
⇔ m = 1.

Dạng 3: Biện luận theo đòi m số cực kỳ trị của hàm số

Đối với cực kỳ trị của hàm số bậc ba

Cho hàm số y = ax^3 + bx^2 + cx + d, a ≠ 0. Khi cơ, tao có: y' = 0 ⇔ 3ax^2 + 2bx + c = 0 (1) ; Δ'y' = b^2 - 3ac.

• Phương trình (1) vô nghiệm hoặc đem nghiệm kép thì hàm số đang được mang lại không tồn tại cực kỳ trị.

• Hàm số bậc 3 không tồn tại cực kỳ trị ⇔ b^2 - 3ac ≤ 0

• Phương trình (1) đem nhì nghiệm phân biệt thì hàm số đang được mang lại đem 2 cực kỳ trị.

• Hàm số bậc 3 đem 2 cực kỳ trị ⇔ b^2 - 3ac > 0

Đối với cực kỳ trị của hàm số bậc bốn

Cho hàm số: y = ax^4 + bx^2 + c (a ≠ 0) đem vật dụng thị là (C). Khi cơ, tao có: y' = 4ax^3 + 2bx; y' = 0 ⇔ x = 0 hoặc x^2 = -b/2a.

• (C) mang trong mình 1 điểm cực kỳ trị y' = 0 có một nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.

• (C) đem tía điểm cực kỳ trị y' = 0 đem 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.

Ví dụ:

Tìm m nhằm hàm số nó = x3 + mx + 2 đem cả cực lớn và cực kỳ tè.

Hướng dẫn giải:

Ta có: y' = 3x2 + m → Hàm số nó = x3 + mx + 2 đem cả cực lớn và cực kỳ tè khi và chỉ khi y'= 0 đem nhì nghiệm phân biệt. Vậy m < 0.

Xem thêm: bài văn tả cô giáo hay nhất

Một số bài bác luyện thăm dò cực kỳ trị của hàm số tự động luyện

Đáp án của những bài bác luyện bên trên thứu tự là: 1A; 2D; 3A; 4A; 5A; 6A; 7D; 8D; 9D; 10B; 11C.

Trên đấy là toàn bộ những kỹ năng về cực trị của hàm số tuy nhiên Monkey ham muốn share cho tới độc giả. Hy vọng rằng nội dung bài viết này sẽ hỗ trợ ích cho chính mình phần này việc ôn luyện cho những kỳ đua tiếp đây. Xin được sát cánh đồng hành nằm trong bạn!