trọng tâm của tam giác

Trọng tâm tam giác là 1 điểm nhập tam giác, được xác lập bằng phương pháp lấy gửi gắm điểm của tía đàng trung tuyến. Đường trung tuyến là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Việc xác lập trọng tâm của tam giác rất có thể triển khai theo đòi quá trình sau:
1. Vẽ một tam giác ngẫu nhiên trong giấy hoặc mặt phẳng bằng.
2. Xác ấn định những đỉnh và những cạnh của tam giác.
3. Chọn ngẫu nhiên tía cạnh của tam giác và xác lập trung điểm của từng cạnh cơ.
4. Vẽ đường thẳng liền mạch nối kể từ trung điểm của từng cạnh cho tới đỉnh ứng.
5. Tìm nút giao của tía đường thẳng liền mạch vừa vặn vẽ. Đây đó là trọng tâm của tam giác.
Trọng tâm tam giác sở hữu tầm quan trọng cần thiết trong những công việc xác lập những Điểm sáng hình học tập của tam giác, bao hàm tâm đàng tròn trĩnh nội tiếp và tâm đàng tròn trĩnh nước ngoài tiếp của tam giác. Hình như, trọng tâm còn tồn tại đặc điểm đặc trưng như tỉ trọng và links với một trong những đường thẳng liền mạch không giống nhập tam giác.

Bạn đang xem: trọng tâm của tam giác

Trọng tâm của tam giác là 1 điểm nằm trong tam giác và được xác lập bằng phương pháp gửi gắm điểm của tía đàng trung tuyến của tam giác. Đường trung tuyến của tam giác là đoạn trực tiếp nối từ là 1 đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Để lần trọng tâm của tam giác, tớ cần thiết tuân theo quá trình sau:
- Cách 1: Vẽ một tam giác có tính nhiều năm những cạnh và đỉnh.
- Cách 2: Tìm trung điểm của cạnh loại nhất của tam giác bằng phương pháp lấy nửa phỏng nhiều năm cạnh.
- Cách 3: Vẽ đường thẳng liền mạch nối kể từ trung điểm cạnh loại nhất cho tới đỉnh tam giác ko phía trên cạnh cơ. Làm tương tự động với nhì cạnh còn sót lại của tam giác nhằm tìm ra tía đàng trung tuyến.
- Cách 4: Tìm gửi gắm điểm của tía đàng trung tuyến. Điểm gửi gắm điểm đó là trọng tâm của tam giác.
Vậy trọng tâm của tam giác là 1 điểm nằm trong tam giác và được xác lập bằng phương pháp gửi gắm điểm của tía đàng trung tuyến của tam giác.

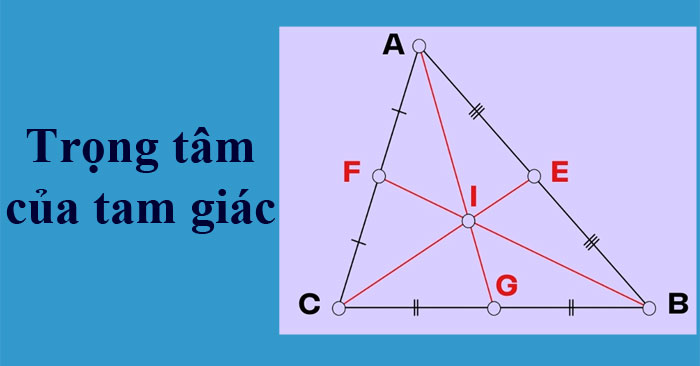
Tam giác sở hữu có một không hai một trọng tâm. Trọng tâm của tam giác đó là gửi gắm điểm của 3 đàng trung tuyến. Đường trung tuyến của một tam giác là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Trên đồ vật thị tam giác, trọng tâm là vấn đề gửi gắm nhau của 3 đàng trung tuyến và nằm sát nhập tam giác.

Cách tính trọng tâm của tam giác như sau:
Bước 1: Tìm điểm trung điểm của từng cạnh của tam giác. Điểm trung điểm là vấn đề ở trung tâm của từng cạnh. Để lần điểm trung điểm, phân chia song phỏng nhiều năm của từng cạnh của tam giác.
Bước 2: Vẽ đường thẳng liền mạch nối những điểm trung điểm. Có tía đàng trung tuyến và bọn chúng hạn chế nhau bên trên một điểm có một không hai.
Bước 3: Điểm ở gửi gắm điểm của tía đàng trung tuyến được gọi là trọng tâm của tam giác.
Ví dụ, cho tới tam giác ABC như sau:
A là vấn đề (-3, 2)
B là vấn đề (4, 6)
C là vấn đề (-2, -5)
Bước 1: Tìm điểm trung điểm của từng cạnh.
Đối với cạnh AB:
Điểm trung điểm của cạnh AB là ((-3 + 4) / 2, (2 + 6) / 2) = (0.5, 4)
Đối với cạnh BC:
Điểm trung điểm của cạnh BC là ((4 - 2) / 2, (6 - 5) / 2) = (1, 0.5)
Đối với cạnh CA:
Điểm trung điểm của cạnh CA là ((-2 - 3) / 2, (-5 + 2) / 2) = (-2.5, -1.5)
Bước 2: Vẽ đường thẳng liền mạch nối những điểm trung điểm.
Vì tớ đang được tìm ra tía điểm trung điểm là (0.5, 4), (1, 0.5), và (-2.5, -1.5), vậy tớ vẽ đường thẳng liền mạch nối tía đặc điểm này.
Bước 3: Tìm nút giao của tía đàng trung tuyến.
Điểm gửi gắm của tía đàng trung tuyến đó là trọng tâm của tam giác.
Qua quá trình đo lường, tớ rất có thể tìm ra tọa phỏng của trọng tâm của tam giác ABC.

Trọng tâm của tam giác là gửi gắm điểm của tía đàng trung tuyến của tam giác cơ. Để lần trọng tâm của tam giác, tớ rất có thể tuân theo quá trình sau đây:
Bước 1: Vẽ tam giác ABC với những đỉnh A, B và C.
Bước 2: Tìm điểm trung điểm M của cạnh AB, điểm trung điểm N của cạnh BC và điểm trung điểm P.. của cạnh AC. Điểm M nằm trong lòng những đỉnh A và B, điểm N nằm trong lòng những đỉnh B và C, và điểm P.. nằm trong lòng những đỉnh A và C.
Bước 3: Vẽ những đàng trung tuyến AM, BN và CP kể từ những đỉnh A, B và C ứng cho tới những điểm trung điểm M, N và P..
Bước 4: Tìm gửi gắm điểm G của tía đàng trung tuyến AM, BN và CP. Điểm G đó là trọng tâm của tam giác ABC.
Vậy, trọng tâm của tam giác ở bên trên điểm G tạo nên tự gửi gắm điểm của tía đàng trung tuyến.

Trọng tâm của tam giác sở hữu tầm quan trọng cần thiết nhập hình học tập. Điểm trọng tâm là vấn đề gửi gắm của tía đàng trung tuyến của tam giác. Đường trung tuyến là đoạn trực tiếp nối trung điểm một cạnh của tam giác với đỉnh đối lập. Vai trò của trọng tâm nhập tam giác là:
1. Trọng tâm là trung tâm của tam giác, là vấn đề tầm của những đỉnh của tam giác. Nghĩa là, nếu như tớ vẽ những đường thẳng liền mạch kể từ trọng tâm cho tới những đỉnh của tam giác, thì tam giác được phân thành tía phần sở hữu diện tích S cân nhau.
2. Trọng tâm phân chia đoạn trực tiếp nối nhì đỉnh của tam giác trở thành nhì phần sở hữu tỉ lệ thành phần tự 2:1. Nghĩa là, nếu như tớ vẽ hai tuyến phố trực tiếp kể từ trọng tâm cho tới nhì đỉnh của tam giác, thì phỏng nhiều năm đoạn trực tiếp kể từ trọng tâm cho tới một đỉnh là nhì phiên phỏng nhiều năm đoạn trực tiếp kể từ trọng tâm cho tới đỉnh còn sót lại.
3. Trọng tâm cũng chính là tâm nhập hình tròn trụ nước ngoài tiếp tam giác. Hình tròn trĩnh nước ngoài tiếp tam giác là hình tròn trụ trải qua toàn bộ tía đỉnh của tam giác. Trọng tâm là trung điểm của đàng chéo cánh của hình tròn trụ nước ngoài tiếp, tức thị đoạn trực tiếp kể từ trọng tâm cho tới trung điểm của một cạnh của tam giác là đàng cao của tam giác cơ.
Vì những Điểm sáng lạ mắt này, trọng tâm của tam giác là 1 điểm cần thiết nhập hình học tập và được dùng nhập thật nhiều Việc và phần mềm.

Đường trung tuyến của tam giác là đàng khởi nguồn từ một đỉnh của tam giác và trải qua trung điểm của cạnh đối lập. Đối với từng đỉnh của tam giác, sở hữu một đàng trung tuyến trải qua kể từ đỉnh cơ cho tới trung điểm của cạnh đối lập. Tam giác sở hữu tía đàng trung tuyến, từng đàng trung tuyến trải qua trung điểm của một cạnh. Trọng tâm của tam giác là gửi gắm điểm của tía đàng trung tuyến cơ. Vấn đề này Có nghĩa là, nếu như tất cả chúng ta vẽ toàn bộ những đàng trung tuyến của tam giác, thì trọng tâm tiếp tục là vấn đề công cộng của toàn bộ những đàng cơ.

Tam giác sở hữu 3 đàng trung tuyến. Mỗi đàng trung tuyến là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Các đàng trung tuyến này gửi gắm nhau bên trên một điểm có một không hai, được gọi là trọng tâm của tam giác. Trọng tâm của tam giác là trung tâm của hình tam giác và là gửi gắm điểm của tía đàng trung tuyến.

Xem thêm: tờ tự kiểm học sinh

Tính hóa học của đàng trung tuyến nhập tam giác là:
- Đường trung tuyến là đoạn trực tiếp nối từ là 1 đỉnh của tam giác cho tới trung điểm của cạnh đối lập.
- Đường trung tuyến hạn chế nhau bên trên một điểm gọi là trọng tâm của tam giác.
- Trọng tâm của tam giác là gửi gắm điểm của tía đàng trung tuyến.
- Trọng tâm phân chia đàng trung tuyến trở thành 2 phần sở hữu tỷ số tự 2:1.
- Trọng tâm là trọng tâm của tam giác, tức là vấn đề trọng tải của tam giác nếu như tam giác được treo lên.
- Đường trung tuyến là hạ tầng cho tới một trong những đặc điểm như: đàng cao của tam giác hạn chế đàng trung tuyến bên trên cung cấp điểm, đàng phân giác của góc hạn chế đàng trung tuyến.

Để vấn đáp thắc mắc này, tất cả chúng ta cần thiết kiểm tra một tam giác ngẫu nhiên và lần hiểu về đàng trung tuyến của tam giác.
Một tam giác sở hữu tía đỉnh là A, B và C. Để dẫn đến một đàng trung tuyến, tớ sử dụng trung điểm của nhì cạnh ngẫu nhiên và nối bọn chúng lại cùng nhau. Ví dụ: muốn tạo rời khỏi đàng trung tuyến AB, tớ lần trung điểm của nhì điểm A và B, ký hiệu là M, tiếp sau đó nối M với đỉnh C.
Đường trung tuyến AB đó là đường thẳng liền mạch AM. Tương tự động, tớ rất có thể dẫn đến đàng trung tuyến BC bằng phương pháp nối trung điểm của B và C, đàng trung tuyến AC bằng phương pháp nối trung điểm của A và C.
Trọng tâm của tam giác đó là gửi gắm điểm của tía đàng trung tuyến này. Nghĩa là, nếu như tớ vẽ đồ vật thị của tam giác và nối tía trung điểm cùng nhau, nút giao của tía đàng này đó là trọng tâm của tam giác.
Tóm lại, đàng trung tuyến của một tam giác rất có thể được dẫn đến bằng phương pháp nối trung điểm của nhì cạnh ngẫu nhiên và trọng tâm của tam giác là gửi gắm điểm của tía đàng trung tuyến này.

Điều khiếu nại nhằm hai tuyến phố trung tuyến hạn chế nhau là lúc tam giác ko nên là tam giác đều. Nếu tam giác là tam giác đều, thì đàng trung tuyến tiếp tục tuy nhiên song cùng nhau và ko hạn chế nhau. Tuy nhiên, nhập tình huống tam giác ko nên tam giác đều, hai tuyến phố trung tuyến tiếp tục hạn chế nhau bên trên một điểm có một không hai, cơ đó là trọng tâm của tam giác. Trọng tâm của tam giác là gửi gắm điểm của tía đàng trung tuyến của tam giác cơ. Đường trung tuyến là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập.

Mối mối liên hệ thân thuộc trọng tâm và đàng trung tuyến nhập tam giác là rằng trọng tâm của tam giác là gửi gắm điểm của tía đàng trung tuyến. Đường trung tuyến của một tam giác là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập.
Đầu tiên, tất cả chúng ta cần thiết nắm rõ định nghĩa về trọng tâm và đàng trung tuyến của tam giác. Trọng tâm của tam giác là 1 điểm có một không hai nằm trong tam giác, được xác lập bằng phương pháp lấy trung điểm của đoạn trực tiếp nối thân thuộc từng đỉnh của tam giác và tâm của đối lập. Đường trung tuyến của tam giác là đoạn trực tiếp nối kể từ từng đỉnh của tam giác cho tới trung điểm của cạnh đối lập.
Qua phân tích và đo lường, đã và đang được chứng tỏ rằng trọng tâm của tam giác đó là nút giao nhau của tía đàng trung tuyến. Vấn đề này Có nghĩa là tía đàng trung tuyến của tam giác hạn chế nhau bên trên một điểm có một không hai, cơ đó là trọng tâm của tam giác.
Tóm lại, quan hệ thân thuộc trọng tâm và đàng trung tuyến nhập tam giác là rằng trọng tâm của tam giác là vấn đề gửi gắm nhau của tía đàng trung tuyến, nhập cơ đàng trung tuyến là đoạn trực tiếp nối kể từ từng đỉnh của tam giác cho tới trung điểm của cạnh đối lập.

Tam giác đều phải có trọng tâm trùng với trung điểm của từng cạnh.
Để chứng tỏ điều này, tất cả chúng ta nên biết rằng trọng tâm của một tam giác đều là gửi gắm điểm của tía đàng trung tuyến của tam giác cơ. Đường trung tuyến là đoạn trực tiếp nối trung điểm của từng cạnh với đỉnh đối lập.
Do tam giác đều phải có tía cạnh cân nhau và có tính nhiều năm như nhau nên trung điểm của từng cạnh của tam giác đều trùng nhau và cũng trùng với trọng tâm của tam giác.
Vì vậy, tam giác đều là tam giác sở hữu trọng tâm trùng với trung điểm của từng cạnh.

Trọng tâm của tam giác sở hữu những đặc điểm đặc trưng sau đây:
1. Trọng tâm của tam giác là vấn đề tầm của tía đỉnh của tam giác. Vấn đề này Có nghĩa là nếu như tớ vẽ những đoạn trực tiếp kể từ trọng tâm cho tới những đỉnh, thì tổng phỏng nhiều năm tía đoạn trực tiếp này cân nhau và tự nhì phiên phỏng nhiều năm những đoạn trực tiếp kể từ trọng tâm cho tới những trung điểm của những cạnh.
2. Trọng tâm của tam giác là gửi gắm điểm của tía đàng trung tuyến. Mỗi đàng trung tuyến là 1 đoạn trực tiếp nối trung điểm của một cạnh của tam giác với đỉnh đối lập.
3. Trọng tâm của tam giác phân chia những đàng trung tuyến theo đòi tỷ trọng 1:2. Nghĩa là đoạn trực tiếp kể từ trọng tâm cho tới trung điểm của một cạnh có tính nhiều năm tự 50% phỏng nhiều năm đoạn trực tiếp kể từ trọng tâm cho tới trung điểm của cạnh đối lập.
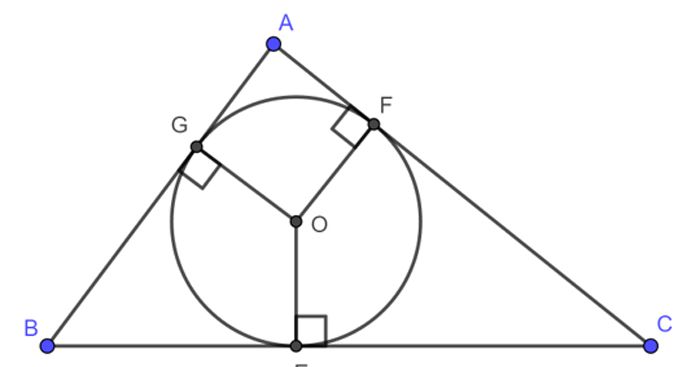
4. Trọng tâm của tam giác cũng chính là tâm đàng tròn trĩnh nước ngoài tiếp tam giác. Đường tròn trĩnh nước ngoài tiếp là đàng tròn trĩnh trải qua tía đỉnh của tam giác. Tâm của đàng tròn trĩnh này là trọng tâm của tam giác.
5. Trọng tâm của tam giác cũng chính là tâm đàng tròn trĩnh nội tiếp tam giác. Đường tròn trĩnh nội tiếp là đàng tròn trĩnh xúc tiếp với tía cạnh của tam giác. Tâm của đàng tròn trĩnh này là trọng tâm của tam giác.
Những đặc điểm đặc trưng này của trọng tâm hỗ trợ chúng ta hiểu và vận dụng trọng tâm nhập việc giải những Việc tương quan cho tới tam giác.

Ứng dụng của trọng tâm tam giác nhập thực tiễn là đặc biệt đa dạng và phổ cập. Dưới đấy là một trong những ví dụ:
1. Xây dựng và loài kiến trúc: Trọng tâm tam giác được dùng nhằm kiến thiết những dự án công trình xây đắp và phong cách thiết kế, như ngôi nhà cửa ngõ, cầu và tòa ngôi nhà. Việc xác lập trọng tâm tam giác hùn hạn chế trọng lực lên những điểm bên trên cạnh tam giác và tăng tính ổn định ấn định của dự án công trình.
2. Thiết kế tiếp dù tô: Trọng tâm tam giác cũng tương đối cần thiết nhập kiến thiết xe hơi. Vị trí trọng tâm tam giác được quan tâm đến nhằm đáp ứng ôtô có tính ổn định ấn định cao và tài năng cân đối chất lượng tốt Khi dịch rời.
3. Thủy văn: Trong nghành thủy văn, trọng tâm tam giác được dùng nhằm đo lường và Dự kiến những dòng sản phẩm chảy nước, hiện tượng kỳ lạ thủy văn. Ví dụ, trọng tâm tam giác rất có thể được dùng nhằm xác lập trọng lượng của vật thể nổi bên trên mặt mày nước.
4. Kỹ thuật ấn định vị: Trọng tâm tam giác cũng khá được dùng nhập nghệ thuật xác định và toán học tập. Việc xác xác định trí trọng tâm tam giác rất có thể hùn xác xác định trí của điểm nhập không khí.
Như vậy, trọng tâm tam giác có tương đối nhiều phần mềm hữu ích nhập thực tiễn, kể từ xây đắp và phong cách thiết kế cho tới nghệ thuật xác định và thủy văn. Việc hiểu và vận dụng công thức tính trọng tâm tam giác rất có thể hùn giải quyết và xử lý một trong những yếu tố thực tiễn một cơ hội hiệu suất cao.

Xem thêm: đô thị hóa là một quá trình