Phương pháp minh chứng nhì tam giác đồng dạng và phần mềm.
Bạn đang xem: chứng minh 2 tam giác đồng dạng
các tình huống đồng dạng của tam giác thông thường :
Trường hợp ý đồng dạng 1 : 3 cạnh ứng tỉ lệ thành phần với nhau (c – c – c)
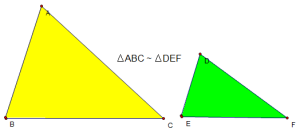
xét ∆ABC và ∆DEF, tao sở hữu :
=> ∆ABC ~ ∆DEF (c – c – c)
Trường hợp ý đồng dạng 2 : 2 cạnh ứng tỉ lệ thành phần cùng nhau – góc xen thân mật nhì cạnh vì thế nhau(c – g – c)
xét ∆ABC và ∆DEF, tao sở hữu :
=> ∆ABC ~ ∆DEF (c – g – c)
Trường hợp ý đồng dạng 3 : nhì góc ứng vì thế nhau(g – g)
xét ∆ABC và ∆DEF, tao sở hữu :
=> ∆ABC ~ ∆DEF (g – g)
II > Các quyết định lí đồng dạng của nhì tam giác vuông
1. Định lí 1 : (cạnh huyền – cạnh góc vuông)
Nếu cạnh huyền và cạnh góc vuông của tam giác này tỉ lệ thành phần với cạnh huyền và cạnh góc vuông của tam giác bại thì nhì tam giác đồng dạng.
2. Định lí 2 : (hai cạnh góc vuông)
Nếu nhì cạnh góc vuông của tam giác này tỉ lệ thành phần với nhì cạnh góc vuông của tam giác bại thì nhì tam giác đồng dạng.
3. Định lí 3 : ( góc)
Nếu góc nhọn của tam giác này vì thế góc nhọn của tam giác bại thì nhì tam giác đồng dạng.
giải bài xích tập luyện :
Dạng 1 : minh chứng nhì tam giác đồng dạng – hệ thức :
Bài toán 1 :
cho ∆ABC (AB < AC), sở hữu AD là đàng phân giác nhập. Tại miền ngoài ∆ABC vẽ tia Cx sao cho . Gọi I là gửi gắm điểm của Cx và AD. cmr :
a) ∆ADB đồng dạng ∆CDI.
b)
c) AD2 = AB.AC – BD.DC
GIẢI.
a)∆ADB và ∆CDI , tao sở hữu :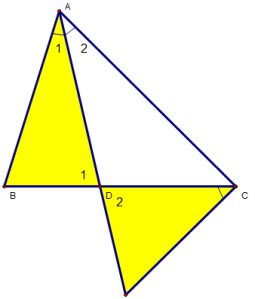
(gt)
(đối đỉnh)
=> ∆ADB ~ ∆CDI
b) )∆ABD và ∆AIC , tao sở hữu :
(∆ADB ~ ∆CDI)
(AD là phân giác)
=> ∆ABD ~ ∆AIC
=>
c)=> AD.AI = AB.AC (1)
mà : (∆ADB ~ ∆CDI )
=> AD.DI = BD.CD (2)
từ (1) và (2) :
AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
bài toán 2 :
Cho tam giác ABC vuông bên trên A, sở hữu đàng cao AH . minh chứng những hệ thức :
- AB2 = BH.BC và AC2 = CH.BC
- AB2 +AC2 = BC2
- AH2 = BH.CH
- AH.BC = AB.AC
Giải.
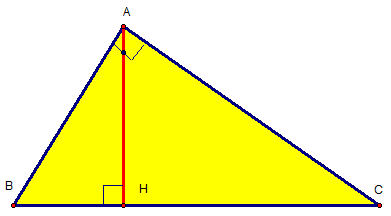
gia su toan lop 8
1. AC2 = CH.BC :
Xét nhì ∆ABC và ∆ HAC, tao sở hữu :
là góc công cộng.
=> ∆ABC ~ ∆HAC (g – g)
=>
=> AC2 = CH.BC (1)
Cmtt : AB2 = BH.BC (2)
2. AB2 +AC2 = BC2
Từ (1) và (2), tao sở hữu :
AB2 +AC2 = BH.BC + CH.BC = (BH + CH)BC = BC2
3.AH2 = BH.CH :
Xét nhì ∆HBA và ∆ HAC, tao sở hữu :
cùng phụ
=> ∆HBA ~ ∆HAC (g – g)
Xem thêm: tác dụng của biện pháp liệt kê
=>
=> AH2 = BH.CH
4. AH.BC = AB.AC :
Ta sở hữu : (∆ABC ~ ∆HAC)
=> AH.BC = AB.AC.
Dạng 2 : minh chứng nhì tam giác đồng dạng – quyết định lí talet + hai tuyến đường trực tiếp tuy vậy song :
bài toán :
Cho ∆ABC nhọn. kẻ đàng cao BD và CE. vẽ những đàng cao DF và EG của ∆ADE. Chứng minh :
a) ∆ABD đồng dạng ∆AEG.
b) AD.AE = AB.AG = AC.AF
c) FG // BC
GIẢI.
a) xét ∆ABD và ∆AEG, tao sở hữu :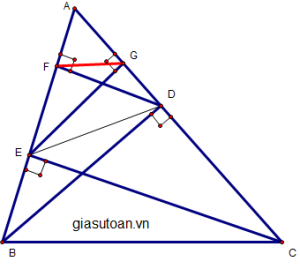
BD AC (BD là đàng cao)
EG AC (EG là đàng cao)
=> BD // EG
=> ∆ABD ~ ∆AGE
b) =>
=> AD.AE = AB.AG (1)
cmtt, tao được : AD.AE = AC.AF (2)
từ (1) và (2) suy rời khỏi :
AD.AE = AB.AG = AC.AF
c) xét ∆ABC, tao sở hữu :
AB.AG = AC.AF (cmt)
=> FG // BC (định lí hòn đảo talet)
Dạng 3 : minh chứng nhì tam giác đồng dạng – góc ứng đều bằng nhau :
bài toán :
Cho ∆ABC sở hữu những đàng cao BD và CE rời nhau bên trên H. Chứng minh :
a) ∆HBE đồng dạng ∆HCE.
b) ∆HED đồng dạng ∆HBC và
c) cho thấy thêm BD = CD. Gọi M là gửi gắm điểm của AH và BC. minh chứng : DE vuông góc EM.
GIẢI.
a)xét ∆HBE và ∆HCD, tao sở hữu :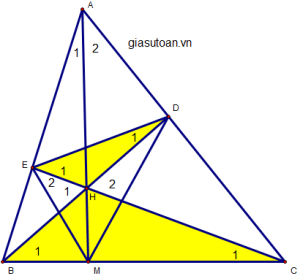
(gt)
(đối đỉnh)
=> ∆HBE ~ ∆HCD (g – g)
b) ∆HED và ∆HBC, tao sở hữu :
(∆HBE ~ ∆HCD)
=>
(đối đỉnh)
=> ∆HED ~ ∆HBC (c – g – c)
=> (1)
mà : đàng cao BD và CE rời nhau bên trên H (gt)
=> H là trực tâm.
=> AH BC bên trên M.
=>
mặt không giống :
=> (2)
từ (1) và (2) :
hay :
c) cmtt câu b, tao được : (3)
xét ∆BCD, tao sở hữu :
DB = DC (gt)
=> ∆BCD cân nặng bên trên D
=>
mà : (∆HED ~ ∆HBC)
=>
mà :
(cmt)
Xem thêm: đề thi đại học môn toán 2022
=>
hay :
=> ED EM.










Bình luận