công thức định lý pytago

By Admin 24/04/2024 0

1. Định lí Pytago Trong một tam giác vuông, bình phương của cạnh huyền bởi vì tổng bình phương nhị cạnh góc vuông.

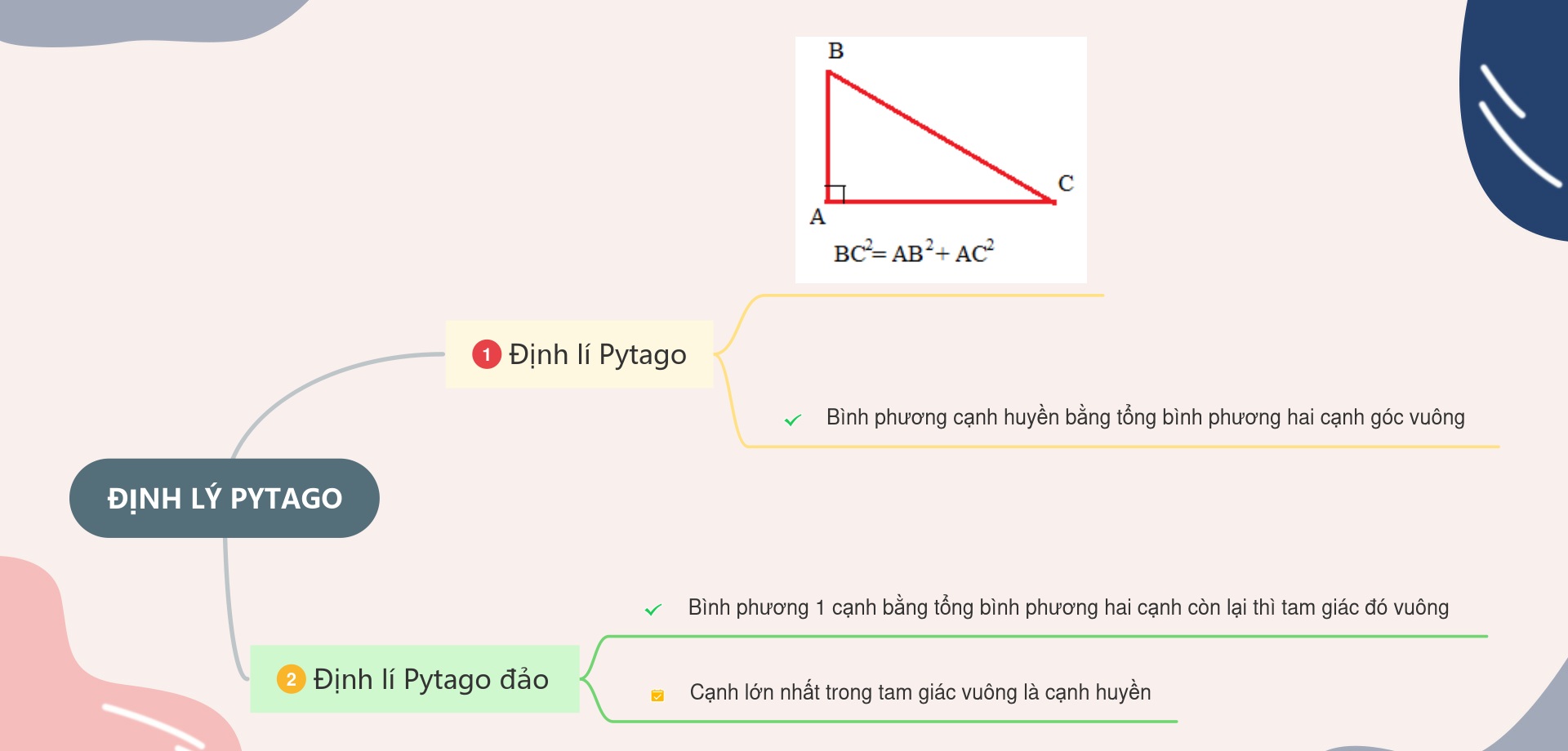
1. Định lí Pytago

Trong một tam giác vuông, bình phương của cạnh huyền bởi vì tổng những bình phương của nhị cạnh góc vuông.

Bạn đang xem: công thức định lý pytago

\(∆ABC\) vuông bên trên \(A\) thì tao có:

\(B{C^2} = A{B^2} + A{C^2}\)

Ví dụ: Cho tam giác ABC vuông bên trên A sở hữu AB= 6cm, AC= 8cm. Tính BC.

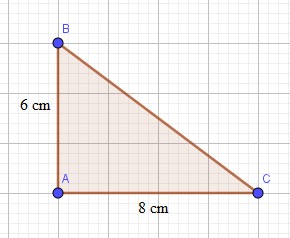
Áp dụng ấn định lí Pytago vô tam giác vuông ABC, tao có:

\(B{C^2} = A{B^2} + A{C^2}\)

Nên \( BC^2= 6^2 + 8^2 = 36+64=100=10^2\)

Vậy \(BC=10 cm\)

Chú ý: Dựa vô ấn định lí Pytago, Khi tao biết phỏng nhiều năm 2 cạnh của tam giác vuông, tao tiếp tục tính được phỏng nhiều năm cạnh còn lại

2. Định lí Pytago hòn đảo.

Nếu một tam giác sở hữu bình phương của một cạnh bởi vì tổng những bình phương của nhị cạnh cơ thì tam giác này đó là tam giác vuông.

\(∆ABC \) có \(B{C^2} = A{B^2} + A{C^2}\)

\(\Rightarrow \widehat {BAC} = {90^o}\)

Sử dụng ấn định lý Py-ta-go hòn đảo nhằm nhận ra tam giác vuông

Phương pháp:

+ Tính bình phương những phỏng nhiều năm tía cạnh của tam giác

Xem thêm: nhiệt độ nóng chảy của nhôm

+ So sánh bình phương của cạnh lớn số 1 với tổng những bình phương của nhị cạnh kia

+ Nếu nhị sản phẩm đều bằng nhau thì tam giác này đó là tam giác vuông, cạnh lớn số 1 là cạnh huyền.

Ví dụ: Cho tam giác ABC sở hữu AC= 5 centimet, BC= 3 centimet, AB= 4 centimet. Tam giác ABC là tam giác gì?

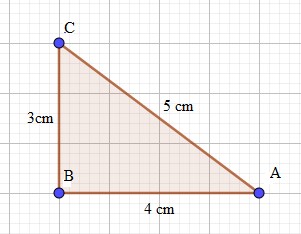
Ta có: \(AC^2 = BC^2+AB^2\)( vì như thế \(5^2=3^2+4^2\))

Nên tam giác ABC vuông bên trên B( Định lí Pytago đảo)

Chú ý: Cạnh huyền là cạnh lớn số 1 vô tam giác vuông


Bình luận

Chia sẻ

>> Xem thêm

Báo lỗi - Góp ý

>> Học trực tuyến lớp 8 bên trên Tuyensinh247.com Đầy đầy đủ khoá học tập những cuốn sách (Kết nối trí thức với cuộc sống; Chân trời sáng sủa tạo; Cánh diều). Cam kết gom học viên lớp 8 học tập chất lượng tốt, trả trả chi phí khóa học nếu như học tập ko hiệu suất cao.