đường trung tuyến ứng với cạnh huyền

Tính hóa học trung tuyến vô tam giác vuông là đường thẳng liền mạch nối trung điểm của một cạnh của tam giác vuông với đỉnh đối lập của tam giác.
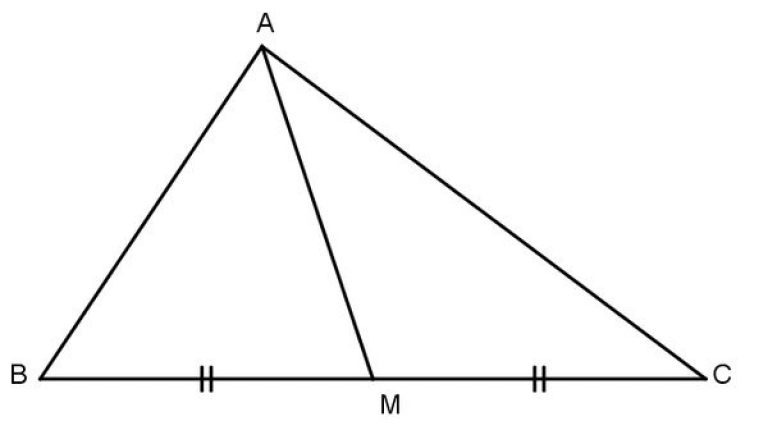
Cụ thể, vô tam giác vuông ABC với cạnh huyền BC, tao ký hiệu trung điểm của cạnh BC là D. Khi bại liệt, đường thẳng liền mạch AD được gọi là trung tuyến của tam giác vuông ABC.
Tính hóa học cần thiết của trung tuyến vô tam giác vuông là độ quý hiếm chừng lâu năm của trung tuyến AD tự 50% chừng lâu năm cạnh huyền BC. Vấn đề này rất có thể được màn biểu diễn tự công thức:
AD = một nửa BC
Nghĩa là chừng lâu năm của đường thẳng liền mạch AD tự 50% chừng lâu năm của cạnh huyền BC.
Trên hạ tầng đặc thù này, tất cả chúng ta rất có thể dùng trung tuyến vô tam giác vuông nhằm giải quyết và xử lý những việc tương quan cho tới tỉ trọng và phân đoạn.

Bạn đang xem: đường trung tuyến ứng với cạnh huyền

Tính hóa học trung tuyến vô tam giác vuông là đường thẳng liền mạch nối trung điểm của một cạnh của tam giác với đỉnh ứng bên trên cạnh sót lại. Cụ thể, vô tam giác vuông ABC với cạnh huyền AB, tao với lối trung tuyến AM, nối đỉnh A với trung điểm M của cạnh BC.
Theo đặc thù trung tuyến vô tam giác vuông, đường trung tuyến ứng với cạnh huyền của tam giác vuông sẽ sở hữu chừng lâu năm tự 50% chừng lâu năm cạnh huyền bại liệt.
Ví dụ, nếu như cạnh huyền AB của tam giác vuông ABC có tính lâu năm là a, thì lối trung tuyến AM sẽ sở hữu chừng lâu năm tự a/2. Đây là đặc thù cần thiết vô tam giác vuông nhưng mà tất cả chúng ta rất có thể dùng nhằm giải quyết và xử lý những việc hình học tập tương quan cho tới tam giác vuông.

Tam giác vuông với 3 trung tuyến.

Mối mối quan hệ thân thuộc trung tuyến và cạnh huyền vô tam giác vuông là:
Trong một tam giác vuông ABC, huyền là cạnh đối lập với góc vuông. Trung tuyến là đoạn trực tiếp nối trung điểm của cạnh huyền với đỉnh góc vuông.
1. Quy ước: Trong tam giác vuông ABC, huyền là cạnh c, những cạnh góc vuông là a và b. Trung tuyến kẻ kể từ đỉnh góc vuông A cho tới trung điểm M của cạnh huyền c.
2. Mối quan liêu hệ: Trung tuyến ứng với cạnh huyền vô tam giác vuông có tính lâu năm tự 50% chừng lâu năm cạnh huyền. Tức là AM = MC = c/2.
Giải thích: Do M là trung điểm của cạnh huyền c, nên theo dõi đặc thù của trung điểm, tao với AM = MC = c/2.
Đây là một trong đặc thù cơ phiên bản của tam giác vuông và rất có thể được dùng trong những việc tương quan cho tới tam giác vuông nhằm tính những độ quý hiếm tương quan cho tới trung tuyến và cạnh huyền.
Ví dụ:
- Nếu cần thiết tính chừng lâu năm trung tuyến vô tam giác vuông khi vẫn biết chừng lâu năm cạnh huyền, tao rất có thể dùng quy tắc này. Ví dụ, nếu như huyền có tính lâu năm là 10, tao rất có thể tính được chừng lâu năm trung tuyến là 10/2 = 5.
- Nếu vẫn biết chừng lâu năm trung tuyến, tao rất có thể tính được chừng lâu năm cạnh huyền. Ví dụ, nếu như trung tuyến có tính lâu năm là 6, tao rất có thể tính được chừng lâu năm cạnh huyền là 6*2 = 12.
Tổng kết, quan hệ thân thuộc trung tuyến và cạnh huyền vô tam giác vuông là chừng lâu năm trung tuyến tự 50% chừng lâu năm cạnh huyền.

Để đo lường và tính toán lối trung tuyến vô tam giác vuông, tao rất có thể tuân theo quá trình sau:
Bước 1: Xác ấn định tam giác vuông và những cạnh của tam giác (đáng xem xét là cạnh huyền).
Bước 2: Tìm trung điểm của cạnh huyền. Đây được xem là kí thác điểm của nhị cạnh kiến thiết trở thành cạnh huyền của tam giác.
Bước 3: Vẽ lối trung tuyến kể từ đỉnh của tam giác cho tới trung điểm cạnh huyền.
Bước 4: Tính chừng lâu năm lối trung tuyến bằng phương pháp dùng quy tắc: Đường trung tuyến ứng với cạnh huyền của tam giác vuông tự 50% cạnh huyền.
Ví dụ:
Giả sử tao với tam giác vuông ABC, vô bại liệt AB là cạnh huyền của tam giác.
Bước 1: Xác ấn định tam giác ABC và những cạnh của tam giác.
Bước 2: Tìm trung điểm của cạnh huyền. Gọi trung điểm của cạnh BC là M.
Bước 3: Vẽ lối trung tuyến kể từ đỉnh của tam giác, tức là đường thẳng liền mạch AM.
Bước 4: Tính chừng lâu năm lối trung tuyến. Theo quy tắc, lối trung tuyến AM có tính lâu năm tự 50% cạnh huyền AB.
Lưu ý rằng lối trung tuyến vô tam giác vuông luôn luôn trải qua trung điểm của cạnh huyền và tạo nên trở thành nhị đoạn trực tiếp có tính lâu năm đều nhau khi tách nhau bên trên trung điểm bại liệt.

Xem thêm: cách nhận biết biểu đồ

Đường trung tuyến vô tam giác vuông là đoạn trực tiếp nối đỉnh của tam giác vuông với trung điểm của cạnh đối lập với đỉnh bại liệt. Trong tam giác vuông ABC, với đỉnh A và cạnh đối lập BC, tao nối đỉnh A với trung điểm M của cạnh BC, thì đoạn trực tiếp AM được gọi là lối trung tuyến. Cụ thể, ĐK nhằm tao xác lập lối trung tuyến vô tam giác vuông là tam giác cần với 1 góc vuông ở một đỉnh và đoạn trực tiếp nối đỉnh bại liệt với trung điểm của cạnh đối lập ko qua quýt gốc vuông của tam giác.

Trong tam giác vuông, chỉ tồn tại một lối trung tuyến. Đường trung tuyến vô tam giác vuông là đoạn trực tiếp nối kể từ đỉnh góc vuông cho tới trung điểm của cạnh huyền.

Tính hóa học của lối trung tuyến vô tam giác vuông là đường trung tuyến ứng với cạnh huyền của tam giác vuông tự 50% cạnh huyền bại liệt. Vấn đề này rất có thể được chứng tỏ như sau:
Cho tam giác vuông ABC với cạnh huyền AB và những cạnh góc vuông AC và BC. Khi bại liệt, lối trung tuyến AM nối đỉnh A với trung điểm M của cạnh BC.
Bước 1: Xác định vị trị của cạnh huyền AB và cạnh BC vô tam giác vuông ABC.
Bước 2: Xác ấn định trung điểm M của cạnh BC bằng phương pháp phân chia song chừng lâu năm cạnh BC.
Bước 3: Tính chừng lâu năm lối trung tuyến AM bằng phương pháp dùng công thức tính khoảng cách thân thuộc nhị điểm vô hệ tọa chừng.
Bước 4: So sánh chừng lâu năm lối trung tuyến AM với độ quý hiếm của nửa cạnh huyền AB.
Nếu chừng lâu năm lối trung tuyến AM tự 50% cạnh huyền AB, thì đặc thù trung tuyến vô tam giác vuông được xác nhận.
Ví dụ: Giả sử AB = 10 centimet và BC = 8 centimet vô tam giác vuông ABC.
Bước 1: Cạnh huyền AB = 10 centimet và cạnh BC = 8 centimet.
Bước 2: Trung điểm M của cạnh BC là thân thuộc nhị điểm B và C, nên chừng lâu năm MB và MC đều tự 4 centimet.
Bước 3: Độ lâu năm lối trung tuyến AM rất có thể tính tự công thức d = √[(x2 - x1)^2 + (y2 - y1)^2], vô bại liệt (x1, y1) và (x2, y2) thứu tự là tọa chừng của nhị điểm A và M.
Assuming that A and M have coordinates (0, 0) and (4, 6) respectively, we can calculate the length of AM using the formula: d = √[(4 - 0)^2 + (6 - 0)^2] = √(16 + 36) = √52 ≈ 7.211 centimet.
Bước 4: Độ lâu năm lối trung tuyến AM được xem là 7.211 centimet. So sánh với nửa cạnh huyền AB = 5 centimet.
Vì chừng lâu năm lối trung tuyến AM ko tự 50% cạnh huyền AB, nên đặc thù trung tuyến vô tam giác vuông ko được thỏa mãn nhu cầu vô ví dụ này.
Tổng kết lại, đặc thù của lối trung tuyến vô tam giác vuông là đường trung tuyến ứng với cạnh huyền của tam giác vuông tự 50% cạnh huyền bại liệt.

Tam giác vuông không tồn tại lối trung tuyến trải qua tâm của lối tròn trặn nước ngoài tiếp. Vì lối trung tuyến là đoạn trực tiếp nối một đỉnh của tam giác với trung điểm của cạnh đối lập, vô tam giác vuông, đỉnh đối lập với cạnh huyền phía trên lối tròn trặn nước ngoài tiếp và tâm của lối tròn trặn nước ngoài tiếp là trung điểm của lối cao kẻ kể từ đỉnh vuông góc cho tới cạnh huyền. Vì vậy, lối trung tuyến ko trải qua tâm của lối tròn trặn nước ngoài tiếp vô tam giác vuông.

Xem thêm: lãnh thổ liên bang nga không có kiểu khí hậu nào sau đây

Trong tam giác vuông, lối trung tuyến ứng với cạnh ko thể dùng làm tính những độ quý hiếm không giống của tam giác. Đường trung tuyến chỉ là một trong lối liên kết kể từ đỉnh của tam giác vuông cho tới trung điểm của cạnh vuông góc với đỉnh bại liệt. Đường trung tuyến ko đem vấn đề về tỉ trọng Một trong những cạnh hoặc những góc của tam giác, vì thế ko thể dùng nhằm đo lường và tính toán những độ quý hiếm không giống của tam giác vuông. Để đo lường và tính toán những độ quý hiếm không giống của tam giác vuông, tất cả chúng ta cần dùng những đặc thù khác ví như ấn định lí Pythagoras, những quy tắc cơ phiên bản của tam giác, hoặc công thức của những hàm trigonometric như sin, cos, tan.