hệ thức lượng trong tam giác

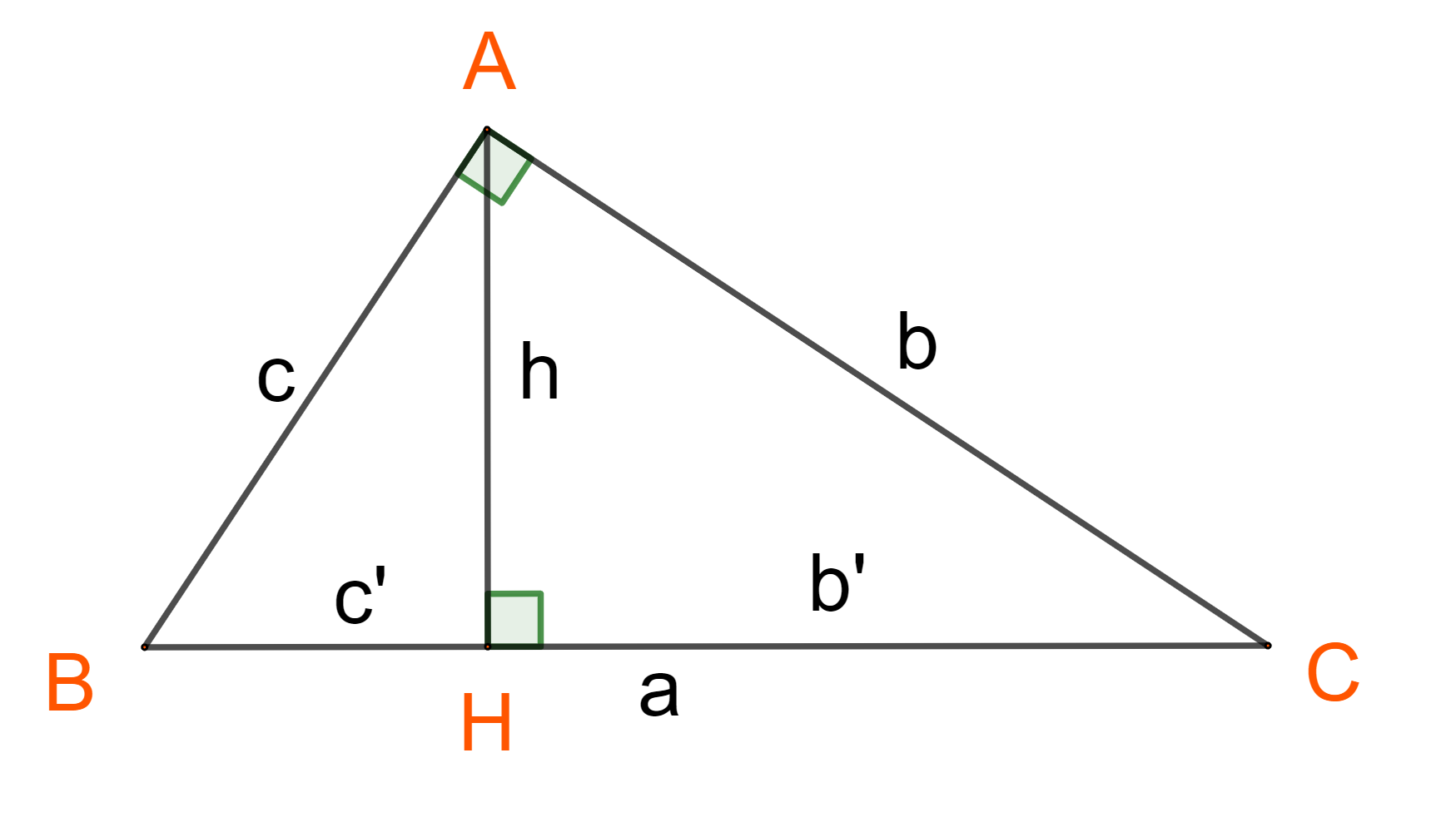
Nhắc lại hệ thức lượng trong tam giác vuông.

Cho tam giác \(ABC\) vuông góc bên trên đỉnh \(A\) (\(\widehat{A} = 90^0\)), tao có:

Bạn đang xem: hệ thức lượng trong tam giác

1. \({b^2} = ab';{c^2} = a.c'\)

2. Định lý Pitago : \({a^2} = {b^2} + {c^2}\)

3. \(a.h = b.c\)

4. \(h^2= b’.c’\)

5. \(\dfrac{1}{h^{2}}\) = \(\dfrac{1}{b^{2}}\) + \(\dfrac{1}{c^{2}}\)

1. Định lý cosin

Định lí: Trong một tam giác bất kì, bình phương một cạnh bởi tổng những bình phương của nhì cạnh còn sót lại trừ chuồn nhì chuyến tích của nhì cạnh cơ nhân với \(cosin\) của góc xen thân thích bọn chúng.

Ta với những hệ thức sau:  

$$\eqalign{
& {a^2} = {b^2} + {c^2} - 2bc.\cos A \, \, (1) \cr
& {b^2} = {a^2} + {c^2} - 2ac.\cos B \, \, (2) \cr
& {c^2} = {a^2} + {b^2} - 2ab.\cos C \, \, (3) \cr} $$

Hệ trái khoáy của toan lí cosin:

\(\cos A = \dfrac{b^{2}+c^{2}-a^{2}}{2bc}\)

\(\cos B = \dfrac{a^{2}+c^{2}-b^{2}}{2ac}\)

\(\cos C = \dfrac{a^{2}+b^{2}-c^{2}}{2ab}\)

Áp dụng: Tính phỏng nhiều năm đàng trung tuyến của tam giác:

Cho tam giác \(ABC\) với những cạnh \(BC = a, CA = b\) và \(AB = c\). Gọi \(m_a,m_b\) và \(m_c\) là phỏng nhiều năm những đàng trung tuyến theo lần lượt vẽ kể từ những đỉnh \(A, B, C\) của tam giác. Ta có

\({m_{a}}^{2}\) =  \(\dfrac{2.(b^{2}+c^{2})-a^{2}}{4}\)

\({m_{b}}^{2}\) = \(\dfrac{2.(a^{2}+c^{2})-b^{2}}{4}\)

\({m_{c}}^{2}\) = \(\dfrac{2.(a^{2}+b^{2})-c^{2}}{4}\)

2. Định lí sin

Định lí: Trong tam giác \(ABC\) ngẫu nhiên, tỉ số thân thích một cạnh và sin của góc đối lập với cạnh cơ bởi 2 lần bán kính của đàng tròn xoe nước ngoài tiếp tam giác, nghĩa là

\(\dfrac{a}{\sin A}= \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R\)

Xem thêm: quần đảo hoàng sa thuộc tỉnh nào

với \(R\) là nửa đường kính đàng tròn xoe nước ngoài tiếp tam giác 

Công thức tính diện tích S tam giác

Diện tích \(S\) của tam giác \(ABC\) được xem theo dõi một trong số công thức sau

\(S = \dfrac{1}{2} ab \sin C= \dfrac{1}{2} bc \sin A \) \(= \dfrac{1}{2}ca \sin B \, \,(1)\)   

\(S = \dfrac{abc}{4R}\, \,(2)\)           

\(S = pr\, \,(3)\)              

\(S = \sqrt{p(p - a)(p - b)(p - c)}\)  (công thức  Hê - rông) \((4)\)

Trong đó:\(BC = a, CA = b\) và \(AB = c\); \(R, r\) là nửa đường kính đàng tròn xoe nước ngoài tiếp, bk đàng tròn xoe nội tiếp và \(S\) là diện tích S tam giác cơ.

3. Giải tam giác và phần mềm vô việc đo đạc

Giải tam giác : Giải tam giác là đi tìm kiếm những nhân tố (góc, cạnh) chưa chắc chắn của tam giác khi tiếp tục biết một số trong những nhân tố của tam giác cơ.

Muốn giải tam giác tao cần thiết lần côn trùng tương tác trong những góc, cạnh tiếp tục cho tới với những góc, những cạnh chưa chắc chắn của tam giác trải qua những hệ thức đã và đang được nêu vô toan lí cosin, toan lí sin và những công thức tính diện tích S tam giác.

Các vấn đề về giải tam giác: Có 3 vấn đề cơ bạn dạng về gỉải tam giác:

a) Giải tam giác lúc biết một cạnh và nhì góc.

=> Dùng toan lí sin nhằm tính cạnh còn sót lại.

b) Giải tam giác lúc biết nhì cạnh và góc xen giữa

=> Dùng toan lí cosin nhằm tính cạnh loại phụ thân. 

Sau cơ sử dụng hệ trái khoáy của toan lí cosin nhằm tính góc.

c) Giải tam giác lúc biết phụ thân cạnh

Đối với vấn đề này tao dùng hệ trái khoáy của toan lí cosin nhằm tính góc: 

    \(\cos A = \dfrac{b^{2}+c^{2}-a^{2}}{2bc}\)       

    \(\cos B = \dfrac{a^{2}+c^{2}-b^{2}}{2ac}\)

    \(cos C = \dfrac{a^{2}+b^{2}-c^{2}}{2ab}\)

Chú ý: 

Xem thêm: đỉnh phan xi păng cao bao nhiêu mét

1. Cần chú ý là một trong tam giác giải được khi tao biết 3 nhân tố của chính nó, vô cơ nên với tối thiểu một nhân tố phỏng nhiều năm (tức là nhân tố góc ko được vượt lên trên 2)

2. Việc giải tam giác được dùng vô những vấn đề thực tiễn, nhất là những vấn đề đo lường.