Chủ đề diện tích S xung xung quanh hình nón: Diện tích xung xung quanh hình nón là một trong những định nghĩa cần thiết nhập hình học tập, canh ty tất cả chúng ta đo lường diện tích S mặt phẳng của hình nón một cơ hội đơn giản dễ dàng. phẳng phiu cơ hội dùng công thức đơn giản và giản dị, tớ rất có thể tính được diện tích S xung xung quanh hình nón bằng phương pháp nhân nửa đường kính lòng của nón với lối sinh và π (3.14). Việc đo lường này canh ty tất cả chúng ta làm rõ rộng lớn về những đặc điểm của hình nón và vận dụng nhập thực tiễn.
Công thức tính diện tích S xung xung quanh hình nón là gì?
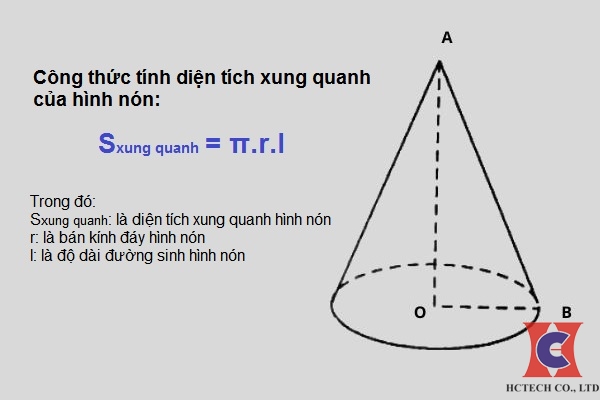
Công thức tính diện tích S xung xung quanh hình nón là S xung xung quanh = π * r * l, nhập đó:
- S xung xung quanh là diện tích S xung xung quanh hình nón.
- π là số Pi, có mức giá trị là khoảng tầm 3.14.
- r là nửa đường kính lòng của hình nón.
- l là lối sinh của hình nón.
Bước 1: Xác ấn định nửa đường kính lòng của hình nón.
Bán kính lòng của hình nón thông thường được cho tới sẵn nhập đề bài xích. Nếu không tồn tại sẵn, chúng ta cũng có thể tính bằng phương pháp lấy 2 lần bán kính lòng phân tách cho tới 2.
Bước 2: Xác ấn định lối sinh của hình nón.
Đường sinh của hình nón là đoạn trực tiếp kể từ tâm lòng của hình nón tới điểm bên trên mép của hình nón. Nó rất có thể được xem bằng phương pháp dùng ấn định lý Pytago: l = √(r^2 + h^2), nhập cơ r là nửa đường kính lòng, h là độ cao của hình nón.
Bước 3: Tính diện tích S xung xung quanh hình nón.
Áp dụng công thức S xung xung quanh = π * r * l, thay cho những độ quý hiếm đang được xác lập nhập công thức nhằm tính được diện tích S xung xung quanh hình nón.
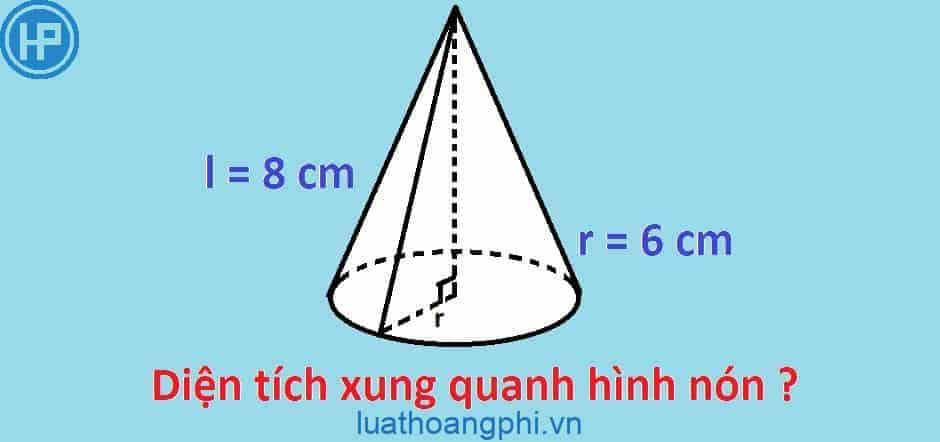
Ví dụ: Cho hình nón đem nửa đường kính lòng là 5 centimet và độ cao là 10 centimet.
Bước 1: Bán kính lòng của hình nón là 5 centimet.
Bước 2: Đường sinh của hình nón là l = √(5^2 + 10^2) = √(25 + 100) = √125 ≈ 11.18 centimet.
Bước 3: Diện tích xung xung quanh hình nón là S xung xung quanh = π * 5 * 11.18 ≈ 175.93 cm^2.
Vậy diện tích S xung xung quanh hình nón là khoảng tầm 175.93 cm^2.
Bạn đang xem: s toàn phần hình nón

Hình nón là gì và đem những bộ phận nào?
Hình nón là một trong những hình học tập đem lòng là một trong những lối tròn xoe và những đường thẳng liền mạch kể từ toàn bộ những điểm bên trên lối tròn xoe lòng cho tới một điểm thắt chặt và cố định phía trên trục đối xứng của lòng. Hình nón bao gồm nhì bộ phận đó là lòng và xung xung quanh.
- Đáy của hình nón là một trong những lối tròn xoe đem nửa đường kính R. Diện tích của lòng hình nón rất có thể tính bởi công thức: Sđ = πR², nhập cơ π là một trong những hằng số xấp xỉ bởi 3.14.
- Xung xung quanh của hình nón là phần bên phía ngoài mặt phẳng hình nón. Diện tích xung xung quanh hình nón rất có thể tính bởi công thức: Sxq = πRl, nhập cơ R là nửa đường kính lòng, và l là lối sinh hình nón. Đường sinh của hình nón được xem bởi công thức: l = √(R² + h²), nhập cơ h là độ cao của hình nón.
- Tổng diện tích S của hình nón bao hàm diện tích S lòng và diện tích S xung quanh: S = Sđ + Sxq.
Về cơ phiên bản, hình nón bao gồm nhì trở nên phần: lòng và xung xung quanh. Đáy của hình nón là một trong những lối tròn xoe đem nửa đường kính R, còn xung xung quanh là phần bên phía ngoài mặt phẳng hình nón.
Như thế này là diện tích S xung xung quanh hình nón?
Diện tích xung xung quanh hình nón là tổng diện tích S của toàn bộ những mặt mũi mặt của hình nón. Để tính diện tích S xung xung quanh hình nón, tất cả chúng ta rất có thể dùng công thức sau:
Diện tích xung xung quanh hình nón (Sxungquanh) = π x nửa đường kính lòng (r) x lối sinh hình nón (l)
Trong đó:
- π là một trong những hằng số xấp xỉ bởi 3.14
- nửa đường kính lòng (r) là chừng nhiều năm kể từ tâm cho tới ngẫu nhiên điểm này bên trên lối viền lòng của hình nón
- lối sinh hình nón (l) là chừng nhiều năm kể từ đỉnh của hình nón tới điểm bên trên lối viền lòng tạo ra với lối sinh một góc vuông
Để tính diện tích S xung xung quanh hình nón, tớ nên biết nửa đường kính lòng và lối sinh của hình nón. quý khách rất có thể nhìn thấy những vấn đề này kể từ vấn đề rõ ràng hoặc kể từ những vấn đề được cung ứng.
Sau Lúc có mức giá trị của nửa đường kính lòng và lối sinh, tớ rất có thể vận dụng công thức bên trên nhằm tính diện tích S xung xung quanh hình nón.
Ví dụ:
Cho hình nón đem nửa đường kính lòng r = 10 và lối sinh l = 16, tớ rất có thể tính diện tích S xung xung quanh hình nón theo gót công thức sau:
Sxungquanh = 3.14 x 10 x 16 = 502.4
Vậy diện tích S xung xung quanh hình nón là 502.4 đơn vị chức năng diện tích S (đơn vị tuỳ nằm trong nhập đơn vị chức năng của nửa đường kính và lối sinh được sử dụng).

Công thức tính diện tích S xung xung quanh hình nón là gì?
Công thức tính diện tích S xung xung quanh hình nón là Sxung xung quanh = πrℓ, nhập cơ r là nửa đường kính lòng hình nón và ℓ là lối sinh hình nón.
Bước 1: Xác ấn định nửa đường kính hình nón (r) và lối sinh hình nón (ℓ).
Bước 2: Tính diện tích S xung xung quanh hình nón bởi công thức Sxung xung quanh = πrℓ. Thay những độ quý hiếm đang được xác lập nhập công thức này.
Ví dụ: Giả sử nửa đường kính lòng hình nón là 5 centimet và lối sinh hình nón là 10 centimet.
Step 1: Xác ấn định r = 5 centimet và ℓ = 10 centimet.
Bước 2: Tính diện tích S xung xung quanh hình nón bởi công thức Sxung xung quanh = πrℓ. Thay những độ quý hiếm nhập công thức này: Sxung xung quanh = π * 5 centimet * 10 centimet = 50π cm^2.
Vậy, diện tích S xung xung quanh hình nón là 50π cm^2.
Bán kính lòng hình nón đem hiệu quả ra sao cho tới diện tích S xung xung quanh của nó?
Bán kính lòng hình nón đem hiệu quả thẳng cho tới diện tích S xung xung quanh của chính nó.
Công thức tính diện tích S xung xung quanh hình nón là Sxungquanh = πrL, nhập cơ r là nửa đường kính lòng và L là lối sinh hình nón.
1. Nếu nửa đường kính lòng tăng thêm, diện tích S xung xung quanh tiếp tục tăng theo gót. Vì Lúc nửa đường kính lòng càng rộng lớn, chu vi lòng cũng càng rộng lớn, kể từ cơ thực hiện tăng diện tích S xung xung quanh theo gót công thức S = πrL.
2. Nếu nửa đường kính lòng sụt giảm, diện tích S xung xung quanh cũng thuyên giảm. Vì Lúc nửa đường kính lòng nhỏ rộng lớn, chu vi lòng cũng tách, kể từ cơ thực hiện tách diện tích S xung xung quanh.
Vậy, nửa đường kính lòng hình nón đem tác động thẳng cho tới diện tích S xung xung quanh của chính nó.
_HOOK_
Hình nón, Hình nón cụt, Diện tích xung xung quanh và thể tích của hình nón, hình nón cụt - Toán 9
Xem Clip về hình nón nhằm tò mò vẻ rất đẹp khác biệt của hình học tập này. quý khách tiếp tục thám thính hiểu về kiểu cách tính diện tích S xung xung quanh hình nón và vận dụng kỹ năng nhập những vấn đề thực tiễn. Hãy tò mò sự thú vị của hình nón tức thì hôm nay!
Hình 12 - Chương 2 - Diện tích xung xung quanh của Nón tròn xoe xoay - Chứng minh công thức
Nếu mình thích làm rõ rộng lớn về nón tròn xoe xoay và công thức tính diện tích S xung xung quanh, hãy coi Clip này ngay! quý khách sẽ tiến hành chỉ dẫn phương pháp tính diện tích S xung xung quanh hình nón một cơ hội đơn giản và giản dị, dễ nắm bắt. Hãy tò mò với công ty chúng tôi tức thì bây giờ!
Chu vi lối tròn xoe lòng và lối sinh của hình nón đem mối quan hệ với diện tích S xung quanh?
Chu vi lối tròn xoe lòng (C) và lối sinh (l) của hình nón đem quan hệ với diện tích S xung xung quanh (Sx) của hình nón.
Công thức tính diện tích S xung xung quanh hình nón là:
Sx = π * r * l
Trong cơ,
- π là số Pi, có mức giá trị xấp xỉ 3.14159,
- r là nửa đường kính lòng của hình nón,
- l là lối sinh của hình nón.
Để tính diện tích S xung xung quanh của hình nón, tớ nên biết nửa đường kính lòng và lối sinh.
- Bán kính lòng hình nón rất có thể tính bởi nửa chu vi lối tròn xoe lòng (C/2π). Vì vậy, tớ rất có thể nhân nửa chu vi lối tròn xoe lòng với 2π nhằm tính nửa đường kính đáy:
r = (C/2π) * 2π = C
- Đường sinh của hình nón rất có thể tính bằng phương pháp dùng công thức lối sinh của hình trụ, này là căn bậc nhì của tổng bình phương nửa đường kính lòng và độ cao hình nón (l = √(r^2 + h^2)).
Tóm lại, nhằm tính diện tích S xung xung quanh của hình nón, tớ nên biết chu vi lối tròn xoe lòng và độ cao hình nón. Sau cơ, tớ dùng công thức Sx = π * r * l nhằm tính diện tích S xung xung quanh.
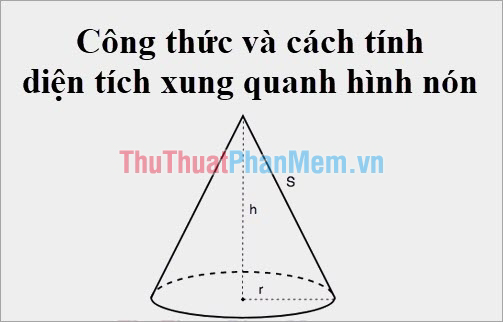
Làm thế này nhằm tính diện tích S xung xung quanh hình nón Lúc chỉ mất nửa đường kính đáy?
Để tính diện tích S xung xung quanh hình nón Lúc chỉ mất nửa đường kính lòng, tớ rất có thể dùng công thức sau:
1. Tính chu vi lối tròn xoe lòng (C):
Chu vi lối tròn xoe lòng bởi công thức C = 2πr, nhập cơ r là nửa đường kính lòng.
2. Tính diện tích S xung xung quanh (Sx):
Diện tích xung xung quanh hình nón bởi 1/2 tích của chu vi lối tròn xoe lòng với chừng nhiều năm lối sinh (l), tức là Sx = một nửa * C * l.
3. Tính lối sinh (l):
Đường sinh (l) của hình nón rất có thể tính bằng phương pháp dùng ấn định lý Pythagoras. Với 1/2 độ cao (h) của hình nón và nửa đường kính lòng (r), tớ rất có thể tính lối sinh (l) bởi công thức l = √(h^2 + r^2).
Với những độ quý hiếm đang được biết về nửa đường kính lòng (r), tớ rất có thể vận dụng công việc bên trên nhằm tính diện tích S xung xung quanh hình nón.
Có cách thức này không giống nhằm tính diện tích S xung xung quanh hình nón ngoài công thức chu vi lối tròn xoe lòng và lối sinh?
Có, lân cận công thức chu vi lối tròn xoe lòng và lối sinh, tất cả chúng ta cũng rất có thể dùng công thức tính diện tích S xung xung quanh hình nón bằng phương pháp lấy diện tích S tam giác đều được tạo ra trở nên kể từ cạnh mặt mũi và nửa đường kính lòng.
Bước 1: Xác ấn định nửa đường kính lòng (r) và cạnh mặt mũi (l) của hình nón.
Bước 2: Tính diện tích S tam giác đều được tạo ra trở nên kể từ cạnh mặt mũi và nửa đường kính lòng bởi công thức:
Diện tích tam giác = (1/2) x cạnh mặt mũi x nửa đường kính lòng.
Với cách thức này, tất cả chúng ta không nhất thiết phải tính chu vi của lối tròn xoe lòng và lối sinh.
Chẳng hạn, nếu như tất cả chúng ta biết nửa đường kính lòng là 5 và cạnh mặt mũi là 8, tớ rất có thể tính diện tích S xung xung quanh hình nón như sau:
Bước 1: Xác ấn định nửa đường kính lòng (r) = 5 và cạnh mặt mũi (l) = 8.
Bước 2: Tính diện tích S tam giác = (1/2) x 8 x 5 = đôi mươi.
Vậy, diện tích S xung xung quanh hình nón nhập tình huống này là đôi mươi đơn vị chức năng diện tích S.
Toán học tập lớp 9 - Bài 2 - Diện tích xung xung quanh và thể tích hình nón, hình nón cụt - Tiết 1
Nếu các bạn đang được học tập toán lớp 9 và quan hoài cho tới hình nón và diện tích S xung xung quanh, chớ bỏ qua Clip này! quý khách sẽ tiến hành cung ứng kỹ năng cơ phiên bản về hình nón và chỉ dẫn phương pháp tính diện tích S xung xung quanh một cơ hội cụ thể và dễ nắm bắt. Hãy nằm trong tò mò toàn cầu toán học!
Xem thêm: đại học hàng hải điểm chuẩn
Có sự khác lạ gì thân mật diện tích S xung xung quanh và diện tích S toàn cỗ của hình nón?
Diện tích xung xung quanh của hình nón chỉ bao hàm diện tích S những mặt mũi mặt của hình nón, ko bao hàm diện tích S lòng của hình nón. Diện tích xung xung quanh của hình nón được xem bởi công thức S xung xung quanh = π * nửa đường kính lòng * lối sinh hình nón.
Trong Lúc cơ, diện tích S toàn cỗ của hình nón bao hàm diện tích S những mặt mũi mặt cùng theo với diện tích S lòng của hình nón. Diện tích toàn cỗ của hình nón được xem bởi công thức S toàn cỗ = diện tích S xung xung quanh + diện tích S lòng = π * nửa đường kính lòng * (bán kính lòng + lối sinh hình nón).
Do cơ, sự khác lạ thân mật diện tích S xung xung quanh và diện tích S toàn cỗ của hình nón là diện tích S lòng của hình nón.
Hình nón rất cần được đem những ĐK gì nhằm tính diện tích S xung quanh?
Để tính diện tích S xung xung quanh của hình nón, tất cả chúng ta nên biết những thông số kỹ thuật sau:
1. Bán kính lòng hình nón (r): Đây là chừng nhiều năm kể từ trung tâm lòng cho tới ngẫu nhiên điểm bên trên lối viền lòng.
2. Chiều cao của hình nón (h): Đây là chừng nhiều năm kể từ đỉnh của hình nón cho tới mặt mũi phẳng phiu lòng.
Công thức tính diện tích S xung xung quanh hình nón là:
Sxung xung quanh = π * r * l
Trong đó:
- π (pi) là một trong những hằng số xấp xỉ bởi 3.14159.
- l (đường sinh hình nón) là chừng nhiều năm của lối có một không hai kể từ đỉnh của hình nón cho tới ngẫu nhiên điểm này bên trên lối viền lòng. Đường sinh được xem bằng phương pháp dùng Pytago: l = √(r^2 + h^2).
Với những độ quý hiếm r và h đang được biết, tất cả chúng ta chỉ việc thay cho nhập công thức bên trên nhằm tính diện tích S xung xung quanh hình nón.
_HOOK_
Diện tích xung xung quanh hình nón đem tương quan cho tới thể tích của chính nó không?
Diện tích xung xung quanh của hình nón đem tương quan cho tới thể tích của chính nó tuy nhiên ko cần là thể tích của chính nó. Diện tích xung xung quanh của hình nón là tổng diện tích S của mặt phẳng cạnh mặt mũi và lòng của hình nón. Thể tích của hình nón là lượng không khí nhưng mà hình nón lắc, được xem bởi công thức V = 1/3 πr²h, nhập cơ r là nửa đường kính lòng của hình nón và h là độ cao của hình nón. Vì vậy, diện tích S xung xung quanh hình nón không tồn tại tương quan thẳng cho tới thể tích của chính nó.

Hình Nón (Toán 12) - Phần 1/3: Tính Diện Tích và Thể Tích Nón | Thầy Nguyễn Phan Tiến
Bạn đang được học tập toán 12 và cần thiết làm rõ về hình nón, diện tích S và thể tích? Video này sẽ hỗ trợ bạn! quý khách sẽ tiến hành chỉ dẫn cụ thể về kiểu cách tính diện tích S và thể tích nón, và vận dụng kỹ năng nhập những vấn đề thực tiễn. Hãy coi tức thì nhằm tăng vững vàng kỹ năng của mình!
Có thể tính diện tích S xung xung quanh hoặc thể tích hình nón Lúc chỉ biết độ cao và nửa đường kính đáy?
Có thể tính diện tích S xung xung quanh và thể tích của hình nón Lúc chỉ biết độ cao và nửa đường kính lòng. Dưới đấy là phương pháp tính chi tiết:
1. Tính diện tích S xung xung quanh (Sxq) của hình nón:
- kề dụng công thức: Sxq = π * nửa đường kính lòng * lối sinh.
- Trong đó:
- π (pi) là một trong những hằng số ngay sát bởi 3.14.
- Bán kính lòng là 2 lần bán kính của lòng hình nón phân tách cho tới 2.
- Đường sinh là một trong những cạnh của tam giác vuông cân nặng nhập hình nón, rất có thể tính bởi căn bậc nhì của số huyền = nửa đường kính đáy^2 + chiều cao^2.
2. Tính thể tích (V) của hình nón:
- kề dụng công thức: V = (1/3) * π * nửa đường kính đáy^2 * độ cao.
- Trong đó:
- π (pi) cũng là một trong những hằng số ngay sát bởi 3.14.
- Bán kính lòng là 2 lần bán kính của lòng hình nón phân tách cho tới 2.
- Chiều cao là đoạn trực tiếp liên kết đỉnh hình nón với mặt mũi lòng.
Đơn vị diện tích S và thể tích cần được ứng với những đơn vị chức năng dùng để làm đo nửa đường kính lòng và độ cao.
Ưu điểm và phần mềm của công thức tính diện tích S xung xung quanh hình nón.
Công thức tính diện tích S xung xung quanh hình nón là Sxungquanh = πrL, nhập cơ r là nửa đường kính lòng hình nón và L là lối sinh hình nón.
Ưu điểm của công thức này là đơn giản và giản dị và dễ nắm bắt. phẳng phiu cơ hội vận dụng công thức này, tất cả chúng ta rất có thể đo lường diện tích S xung xung quanh hình nón một cơ hội nhanh gọn và đúng mực.
Công thức còn rất có thể được phần mềm trong tương đối nhiều nghành không giống nhau, bao gồm:
1. Architecture: Công thức này rất có thể được dùng nhằm tính diện tích S xung xung quanh những rường cột, hình nón nhập phong cách thiết kế. Vấn đề này canh ty phong cách thiết kế sư đo lường được diện tích S tô, vật tư cần dùng và canh ty xác lập được độ dài rộng đúng mực của những hình nón.
2. Manufacturing: Trong ngành công nghiệp, công thức này rất có thể được vận dụng nhằm đo lường diện tích S mặt phẳng những vật thể hình nón. Vấn đề này tương hỗ quy trình thực hiện kiểu, gia công, hoặc đo lường vật tư quan trọng.
3. Geometry: Công thức tính diện tích S xung xung quanh hình nón là một trong những ví dụ rõ ràng nhập hình học tập không khí. Nó canh ty học viên và SV làm rõ rộng lớn về đặc điểm của hình nón và phương pháp tính toán diện tích S của chính nó.
4. Real-life applications: Công thức này rất có thể được phần mềm nhập thực tiễn nhằm xử lý những yếu tố tương quan cho tới hình nón như đo lường diện tích S mặt mũi sau của một tượng nón, diện tích S xung xung quanh một nón tách bởi một phía phẳng phiu, hoặc diện tích S xung xung quanh một cồn núi đem hình trạng nón.
Tóm lại, công thức tính diện tích S xung xung quanh hình nón là một trong những dụng cụ hữu ích và phần mềm rộng thoải mái trong tương đối nhiều nghành.
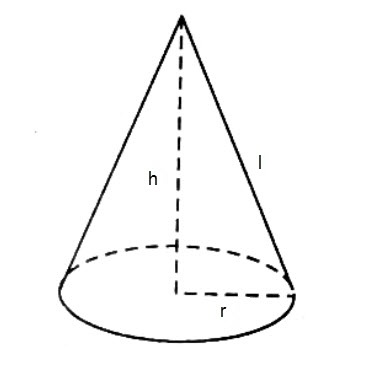
Một ví dụ rõ ràng về kiểu cách tính diện tích S xung xung quanh hình nón.
Để tính diện tích S xung xung quanh của một hình nón, tớ tiếp tục dùng công thức sau:
Diện tích xung xung quanh = π x nửa đường kính lòng x lối sinh
Ví dụ, fake sử tớ mang trong mình một hình nón với nửa đường kính lòng là 3cm và lối sinh là 4cm. Ta tiếp tục vận dụng công thức bên trên nhằm tính diện tích S xung xung quanh.
Bước 1: Xác định vị trị cho tới nửa đường kính lòng và lối sinh.
- Bán kính lòng (r) = 3cm
- Đường sinh (l) = 4cm
Bước 2: kề dụng công thức nhằm tính diện tích S xung xung quanh.
- Diện tích xung xung quanh (A) = π x r x l
Bước 3: Thay nhập độ quý hiếm của r và l.
- A = π x 3cm x 4cm
Bước 4: Tính toán độ quý hiếm.
- A = 3.14 x 3cm x 4cm
- A = 37.68 cm²
Vậy, diện tích S xung xung quanh của hình nón nhập ví dụ này là 37.68 cm².
Có cách thức này nhằm tính diện tích S xung xung quanh hình nón không tồn tại đáy?
Có, tất cả chúng ta rất có thể tính diện tích S xung xung quanh hình nón không tồn tại lòng bởi cách thức sau đây:
1. Tìm chu vi của lối tròn xoe đỉnh của hình nón không tồn tại lòng. Đường tròn xoe này là lối tròn xoe được tạo ra bởi đỉnh và một điểm bên trên lối viền của lòng hình nón. Gọi chu vi này là C.
2. Tính lối sinh của hình nón không tồn tại lòng. Đường sinh là đoạn trực tiếp nối kể từ đỉnh cho tới trung điểm của lối viền lòng của hình nón. Gọi lối sinh là l.
3. kề dụng công thức tính diện tích S xung xung quanh hình nón: S = một nửa * C * l.
Ví dụ:
Giả sử tớ mang trong mình một hình nón không tồn tại lòng với chu vi của lối tròn xoe đỉnh là 10cm và lối sinh là 6cm.
1. Chu vi của lối tròn xoe đỉnh C = 10cm.
2. Đặt lối sinh l = 6cm.
3. Tính diện tích S xung xung quanh hình nón bởi công thức: S = một nửa * 10cm * 6cm = 30cm^2.
Vậy diện tích S xung xung quanh hình nón không tồn tại lòng là 30cm^2.
Xem thêm: công thức tính diện tích hình tròn
_HOOK_
MÔN TOÁN HỌC - LỚP 9 | HÌNH NÓN. DIỆN TÍCH XUNG QUANH VÀ THỂ TÍCH | 9H15 NGÀY 19.05.2020 | HANOITV
Môn Toán Học lớp 9 cung ứng kỹ năng cơ phiên bản về hình nón và diện tích S xung xung quanh. Video này tiếp tục khiến cho bạn cầm được công thức tính diện tích S và vận dụng nhập những vấn đề thực tiễn. Đừng bỏ qua thời cơ học hỏi và chia sẻ và tò mò toán học tập nằm trong bọn chúng tôi!












Bình luận