Tập nghiệm của bất phương trình

Tìm tập nghiệm của bất phương trình lớp 10

Tập nghiệm của bất phương trình môn Toán lớp 10 vừa mới được VnDoc.com thuế tầm và van gửi cho tới độc giả nằm trong tìm hiểu thêm. Mời chúng ta nằm trong theo đòi dõi nội dung bài viết tiếp sau đây.

Bạn đang xem: tập nghiệm của bất phương trình

Tài liệu vì thế VnDoc.com biên soạn và đăng lên, nghiêm khắc cấm những hành động sao chép với mục tiêu thương nghiệp.

Tìm tập nghiệm của bất phương trình

1. Tập nghiệm S của bất phương trình là gì?

Trước không còn tớ xét cho tới khái niệm bất phương trình một ẩn

- Bất phương trình một ẩn là 1 trong mệnh đề chứa chấp trở thành x đối chiếu nhị hàm số f(x) và g(x) bên trên ngôi trường số thực bên dưới một trong số dạng

f(x) < g(x), f(x) > g(x); f(x) ≥ g(x); f(x) ≤ g(x)

- Giao của nhị tập dượt xác lập của những hàm số f(x) và g(x) được gọi là tập dượt xác lập của bất phương trình.

- Nếu với độ quý hiếm x =a, f(a) > 0 là bất đẳng thức chính thì tớ bảo rằng a nghiệm chính bất phương trình f(x) > 0, hoặc a là nghiệm của bất phương trình.

Tập hợp ý toàn bộ những nghiệm của bất phương trình được gọi là tập dượt nghiệm hoặc câu nói. giải của bất phương trình, nhiều lúc nó cũng khá được gọi là miền chính của bất phương trình. Trong nhiều tư liệu người tớ cũng gọi tập nghiệm của bất phương trình là nghiệm của bất phương trình.

Ví dụ Bất phương trình 4.x + 2 > 0 nghiệm chính với từng số thực x > -0.5. Tập nghiệm của bất phương trình là { x ∈ R | x > -0.5 } = (0.5; $\infty$ )

Phân loại bất phương trình:

- Các bất phương trình đại số bậc k là những bất phương trình nhập bại liệt f(x) là nhiều thức bậc k.

- Các bất phương trình vô tỷ là những bất phương trình với chứa chấp luật lệ khai căn

- Các bất phương trình nón là những bất phương trình với chứa chấp hàm nón (chứa trở thành bên trên lũy quá.

- Các bất phương trình logarit là những bất phương trình với chứa chấp hàm logarit (chứa trở thành nhập lốt logarit).

2. Bài tập dượt ví dụ minh họa

Bài tập dượt 1: Tìm tập dượt nghiệm S của bất phương trình $\sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15$

Hướng dẫn giải

Điều khiếu nại xác định: ${x^2} - 5x - 6 \geqslant 0 \Leftrightarrow x \in \left( { - \infty ; - 1} \right] \cup \left[ {6; + \infty } \right)$

Bất phương trình tương đương:
$\begin{matrix} \sqrt {{x^2} - 5x - 6} + 2{x^2} > 10x + 15 \hfill \\ \Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2{x^2} + 10x + 15 \hfill \\ \Leftrightarrow \sqrt {{x^2} - 5x - 6} > - 2\left( {{x^2} - 5x - 6} \right) + 3\left( * \right) \hfill \\ \end{matrix}$
Đặt $\sqrt {{x^2} - 5x - 6} = t;\left( {t \geqslant 0} \right)$ (**)

$\begin{matrix} \left( * \right) \Leftrightarrow t > - 2{t^2} + 3 \hfill \\ \Leftrightarrow 2{t^2} + t - 3 > 0 \hfill \\ \Leftrightarrow t \in \left( { - \infty ; - \dfrac{3}{2}} \right] \cup \left[ {1; + \infty } \right) \hfill \\ \end{matrix}$

Kết phù hợp với ĐK (**) $\Rightarrow t \in \left[ {1; + \infty } \right)$

$\begin{matrix} \Rightarrow \sqrt {{x^2} - 5x - 6} \geqslant 1 \Leftrightarrow {x^2} - 5x - 6 \geqslant 1 \hfill \\ \Rightarrow x \in \left( { - \infty ;\dfrac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\dfrac{{5 + \sqrt {53} }}{2}; + \infty } \right) \hfill \\ \end{matrix}$

Vậy tập nghiệm của bất phương trình là $x \in \left( { - \infty ;\frac{{5 - \sqrt {53} }}{2}} \right] \cup \left[ {\frac{{5 + \sqrt {53} }}{2}; + \infty } \right)$

Bài tập dượt 2: Tìm tập nghiệm của bất phương trình: $\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0$

Hướng dẫn giải

Điều khiếu nại xác lập x² – 6x + 8 ≠ 0 ⟺ x ≠ 2, x ≠ 4

$\frac{{{x^2} - 4}}{{{x^2} - 6x + 8}} \leqslant 0 \Leftrightarrow \frac{{\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x - 4} \right)\left( {x - 2} \right)}} \leqslant 0 \Leftrightarrow \frac{{x + 2}}{{x - 4}} \leqslant 0$

Lập bảng xét lốt tớ có:

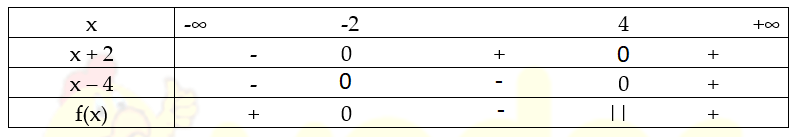
Tập nghiệm của bất phương trình

Từ bảng xét lốt tớ kết luận: Tập nghiệm của bất phương trình là: x ∈ [ -2 ; 4)

Bài tập dượt 3: Giải bất phương trình: (x² + 3x + 1)(x² + 3x – 3) ≥ 5 (*)

Hướng dẫn giải

Tập xác lập D = $\mathbb{R}$

Đặt x² + 3x – 3 = t ⟹ x² + 3x + 1 = t + 4

Bất phương trình (*) ⟺ t(t+4) ≥ 5

⟺ t² + 4t – 5 ≥ 0

Xem thêm: văn tả con chó lớp 4 ngắn gọn nhất

⟺ t ∈ (-∞; -5] ∪ [1; +∞)

$\begin{matrix} \Rightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} + 3x - 3 \leqslant - 5} \\ {{x^2} + 3x - 3 \geqslant 1} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} + 3x + 2 \leqslant 0} \\ {{x^2} + 3x - 4 \geqslant 0} \end{array}} \right. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x \in \left[ { - 2; - 1} \right]} \\ {x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right)} \end{array}} \right. \Rightarrow x \in \left( { - \infty - 4} \right] \cup \left[ {1; + \infty } \right) \hfill \\ \end{matrix}$

Vậy tập nghiệm của bất phương trình là x ∈ (-∞; -4] ∪ [1; +∞)

3. Bài tập dượt tự động rèn luyện

Câu 1: Tìm tập dượt nghiệm S của bất phương trình x²- 4 > 0

A. S = (-2 ; 2).	B. S = (-∞ ; -2) ∪ (2; +∞)
C. S = (-∞ ; -2] ∪ [2; +∞)	D. S = (-∞ ; 0) ∪ (4; +∞)

Câu 2: Tìm tập dượt nghiệm S của bất phương trình x² – 4x + 4 > 0.

A. S = R	B. S = R\{2}
C. S = (2; ∞)	D. S =R\{-2}

Câu 3: Tập nghiệm S = (-4; 5) là tập nghiệm của bất phương trình nào là sau đây?

A. (x + 4)(x + 5) < 0	B. (x + 4)(5x - 25) ≥ 0
C. (x + 4)(x + 25) < 0	D. (x - 4)(x - 5) < 0

Câu 4: Cho biểu thức: f(x) = ax² + bx + c (a ≠ 0) và ∆ = b² – 4ac. Chọn xác định chính trong số xác định bên dưới đây?

A. Khi ∆ < 0 thì f(x) nằm trong lốt với thông số a với từng x ∈ $\mathbb{R}$ .

B. Khi ∆ = 0 thì f(x) trái khoáy lốt với thông số a với từng $x \ne \frac{{ - b}}{{2a}}$ .

C. Khi ∆ < 0 thì f(x) nằm trong lốt với thông số a với từng $x \ne \frac{{ - b}}{{2a}}$ .

D. Khi ∆ > 0 thì f(x) trái khoáy lốt với thông số a với từng x ∈ $\mathbb{R}$ .

Câu 5: Tìm tập nghiệm của bất phương trình: -x² + 2017x + 2018 > 0

A. S = [-1 ; 2018]	B. S = (-∞ ; -1) ∪ (2018; +∞)
C. S = (-∞ ; -1] ∪ [2018; +∞)	D. S = (-1 ; 2018)

Câu 6: Giải những bất phương trình sau:

Câu 7: Tìm tập dượt nghiệm của những bất phương trình sau:

Câu 8: Tập nghiệm S của bất phương trình 5x-1 = ≥ 5x/2 +3 là:

A. S = (+ $\infty$ ; 5)

B. S = (- $\infty$ ;2)

C. S = (-5/2; + $\infty$ )

D. S = (20/23; + $\infty$ )

Câu 9: Bất phương trình $\frac{3x+5}2-1\leq\frac{x+2}3+x$ với từng nào nghiệm nguyên vẹn to hơn -10

A. 4

B. 5

C. 9

D. 10

Câu 10: Tổng những nghiệm nguyên vẹn của bất phương trình x (2-x) ≥ x (7-x) - 6 (x-1) bên trên đoạn (-10;10) bằng:

A. 5

B. 6

C. 21

D. 40

Câu 11: Bất phương trình (m-1) x>3 vô nghiệm khi

A. m≠1

B. m<1

C. m=1

Xem thêm: đề thi toán thpt 2022

D. m>1

--------------------------------------------------------

Trên đó là tư liệu về Cách lần tập dượt nghiệm S của bất phương trình được VnDoc.com ra mắt cho tới quý thầy cô và độc giả nằm trong tìm hiểu thêm. Hy vọng với tư liệu này chúng ta học viên tiếp tục cầm vững chắc kiến thức và kỹ năng áp dụng chất lượng nhập giải bài bác tập dượt kể từ bại liệt học tập chất lượng môn Toán lớp 10.