thể tích khối đa diện

Trong lịch trình toán ganh đua trung học phổ thông Quốc Gia, khối nhiều diện cướp một lượng kiến thức và kỹ năng tương đối lớn, bởi vậy thời điểm ngày hôm nay Kiến Guru nài share cho tới chúng ta phát âm cỗ công thức hình học tập 12 về khối nhiều diện. 

Bạn đang xem: thể tích khối đa diện

Kiến kỳ vọng trải qua nội dung bài viết này, những các bạn sẽ mang 1 tư liệu ôn tập luyện tóm gọn gàng, đúng mực và ăm ắp tính phần mềm. Bài viết lách vừa phải nhắc nhở lại một trong những khái niệm cơ bạn dạng, bên cạnh đó cũng tổ hợp một vài công thức tính nhanh chóng toán 12 về tính chất thể tích. Mời độc giả nằm trong tìm hiểu thêm qua:

1. Khái niệm.

Hình nhiều diện: là hình được dẫn đến bởi vì một trong những hữu hạn vừa lòng nhì tính chất:

+ Hai nhiều giác phân biệt chỉ rất có thể hoặc không tồn tại điểm công cộng, hoặc có duy nhất một đỉnh công cộng, hoặc có duy nhất một cạnh công cộng.

+ Mỗi cạnh của nhiều giác nào thì cũng là cạnh công cộng của đích 2 nhiều giác.

Khối nhiều diện: là phần không khí được số lượng giới hạn bởi vì một hình nhiều diện, bao gồm hình nhiều diện bại.

Khối nhiều diện nếu như được số lượng giới hạn bởi vì hình lăng trụ tiếp tục gọi là khối lăng trụ. Tương tự động, nếu như được số lượng giới hạn bởi vì hình chóp thì gọi là khối chóp,...

Trong đo lường tớ thông thường nói đến khối nhiều diện lồi: tức là 1 khối nhiều diện (H) vừa lòng nếu như nối 2 điểm bất kì của (H) tớ đều nhận được một quãng trực tiếp nằm trong (H).

Cho một nhiều diện lồi, tớ đem công thức Euler về tương tác thân thiện số đỉnh D, số cạnh C và số mặt mũi M: D-C+M=2.

Khối nhiều diện đều là khối nhiều diện lồi đem đặc thù sau đây:

+ Mỗi mặt mũi của chính nó là 1 nhiều giác đều p cạnh.

+ Mỗi đỉnh của chính nó là đỉnh công cộng của đích q mặt mũi.

Một số khối nhiều diện lồi thông thường gặp:

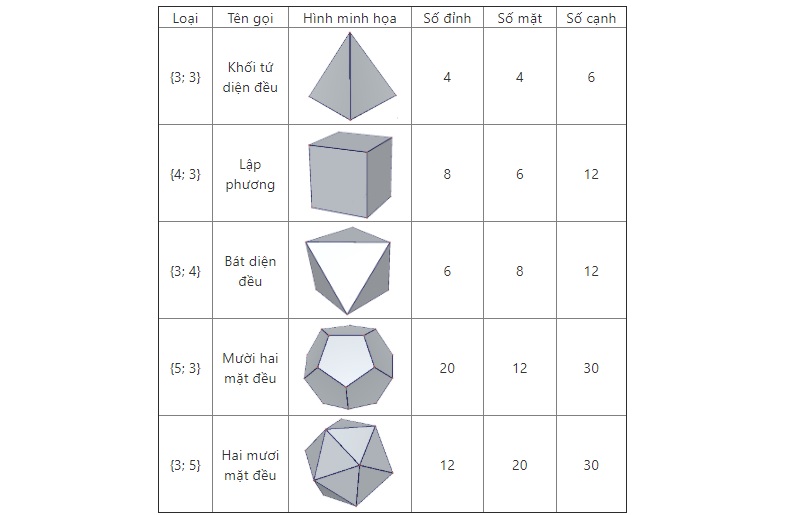
Ví dụ về khối nhiều diện:

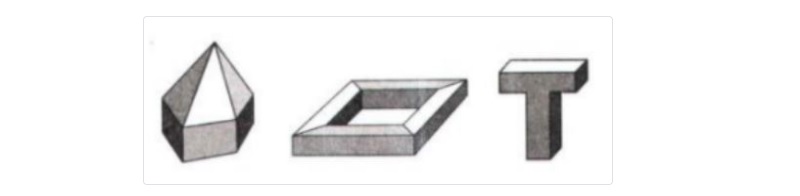
Ví dụ về khối hình ko nên nhiều diện:

2. Phân phân chia, thi công ghép khối nhiều diện.

Những điểm ko nằm trong khối nhiều diện gọi là vấn đề ngoài, tụ hợp những điểm ngoài gọi là miền ngoài. Điểm nằm trong khối nhiều diện tuy nhiên ko phía trên hình nhiều diện bao ngoài được gọi là vấn đề nhập khối nhiều diện, tương tự động, tụ hợp những điểm nhập tạo ra miền nhập khối nhiều diện.

Cho khối nhiều diện (H) là phù hợp của nhì khối nhiều diện (H1) và (H2) vừa lòng, (H1) và (H2) không tồn tại điểm công cộng nhập này thì tớ rằng (H) rất có thể phần phân chia được trở thành 2 khối (H1) và (H2), bên cạnh đó cũng nói theo cách khác ghép nhì khối (H1) và (H2) nhằm nhận được khối (H).

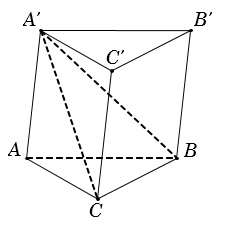
Ví dụ: Cắt lăng trụ ABC.A’B’C’ bởi vì mặt mũi phẳng lì (A’BC) tớ nhận được nhì khối nhiều diện mới mẻ A’ABC và A’BCC’B’.

Xem thêm: tính oxi hóa là gì

3. Một số thành quả cần thiết.

KQ1: cho 1 khối tứ diện đều:

+ Trọng tâm của những mặt mũi là đỉnh của một khối tứ diện đều không giống.

+ Trung điểm của những cạnh của chính nó là những đỉnh của một khối chén diện đều (khối tám mặt mũi đều).

KQ2: Cho khối lập phương, tâm những mặt mũi của chính nó sẽ khởi tạo trở thành 1 khối chén diện đều.

KQ3: Cho khối chén diện đều, tâm những mặt mũi của chính nó sẽ khởi tạo trở thành một khối lập phương.

KQ4: Hai đỉnh của một khối chén diện đều được gọi là nhì đỉnh đối lập nếu như bọn chúng ko nằm trong phụ thuộc một cạnh của khối bại. Đoạn trực tiếp nối nhì đỉnh đối lập gọi là lối chéo cánh của khối chén diện đều. Khi đó:

+ Ba lối chéo cánh rời nhau bên trên trung điểm của từng lối.

+ Ba lối chéo cánh song một vuông góc cùng nhau.

+ Ba lối chéo cánh đều bằng nhau.

KQ5: một khối nhiều diện nên đem ít nhất 4 mặt mũi.

KQ6: HÌnh nhiều diện đem ít nhất 6 cạnh.

KQ7: Không tồn trên rất nhiều diện đem 7 cạnh.

II. Tổng phù hợp công thức hình học tập 12 thể tích khối đa diện.

1. Thể tích khối chóp:

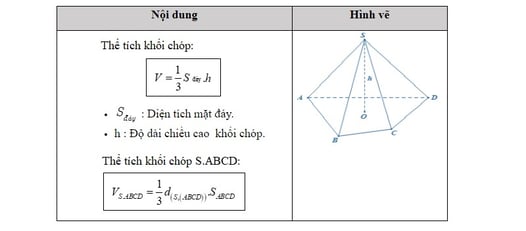
2. Thể tích khối lăng trụ:

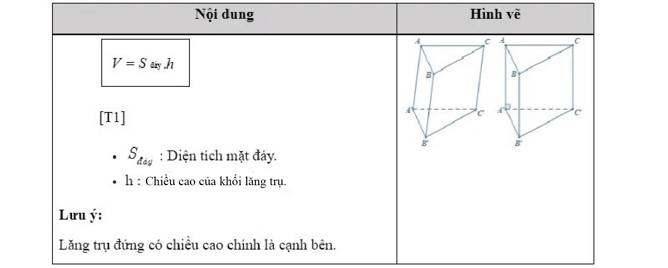
3. Thể tích khối vỏ hộp chữ nhật:

Chú ý: Hình lập phương là một hình hộp chữ nhật có các cạnh bằng nhau.

4. Công thức tỉ số thể tích

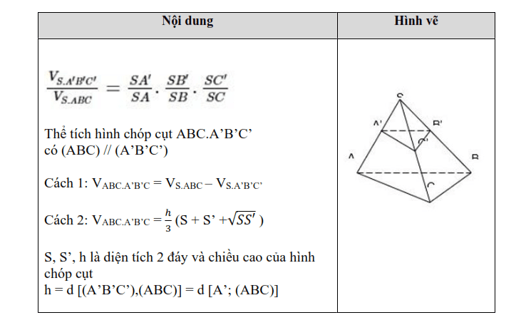
Chú ý quánh biệt: công thức về tỷ số thể tích chỉ được sử dụng mang đến khối chóp tam giác. Nếu bắt gặp khối chóp tứ giác, tớ cần thiết phân chia nhỏ trở thành 2 khối chóp tam giác nhằm vận dụng công thức này.

5. Công thức tính nhanh chóng toán 12 một trong những lối quánh biệt:

Đường chéo cánh của hình lập phương cạnh a có tính dài: 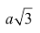SS

Cho hình vỏ hộp có tính lâu năm 3 cạnh là a, b, c thì chừng lâu năm lối chéo cánh là: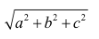

Đường cao của tam giác đều cạnh a là: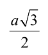

Ngoài đi ra, nhằm tính thể tích khối đa diện, lưu ý một trong những công thức toán hình phẳng lì sau:

Cho tam giác vuông ABC bên trên A, xét lối cao AH. Khi đó:

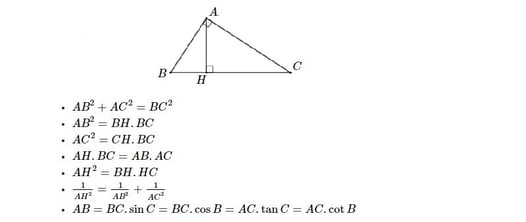
Xem thêm: bác hồ bao nhiêu tuổi

Công thức tính diện tích S tam giác ABC có tính lâu năm 3 cạnh là a,b,c; a lối cao ứng là h_a, h_b, h_c; nửa đường kính lối tròn
ngoại tiếp là R; nửa đường kính lối tròn trĩnh nội tiếp là r; nửa chu vi tam giác là

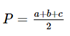
Trên đó là những tổ hợp của Kiến về công thức hình học tập 12 đề chính thể tích khối đa diện. Hy vọng trải qua nội dung bài viết, những các bạn sẽ ôn tập luyện, nâng lên được kiến thức và kỹ năng của bạn dạng thân thiện. Mỗi dạng toán đều cần thiết sự góp vốn đầu tư chỉnh chu, bởi vậy ghi lưu giữ công thức một cơ hội đúng mực cũng chính là phương pháp để nâng cao điểm vào cụ thể từng bài bác ganh đua. Bên cạnh đó chúng ta cũng rất có thể tìm hiểu thêm thêm thắt những nội dung bài viết không giống của Kiến để sở hữu thêm thắt nhiều điều có lợi. Chúc chúng ta như mong muốn.