Nếu nhị tiếp tuyến của một lối tròn trặn hạn chế nhau bên trên một điểm thì:
Tổng hợp ý đề ganh đua học tập kì 1 lớp 9 toàn bộ những môn
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD
Bạn đang xem: tính chất hai tiếp tuyến cắt nhau
LÝ THUYẾT VỀ TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU
1. Tính hóa học nhị tiếp tuyến hạn chế nhau
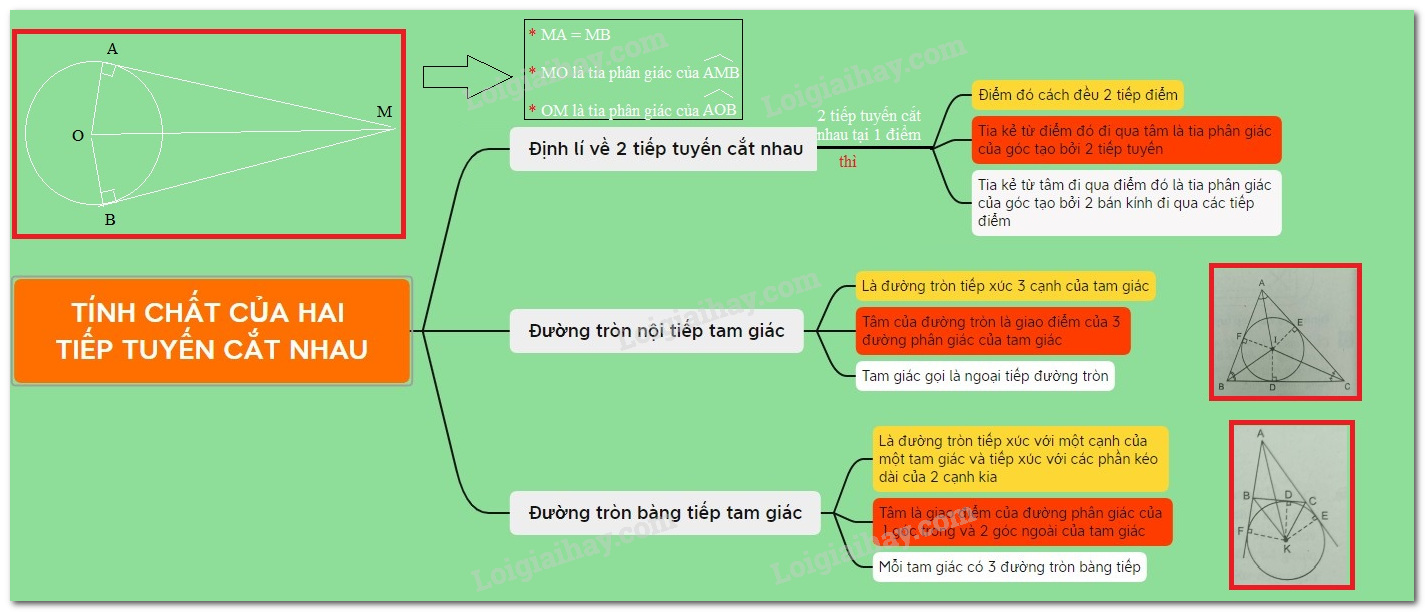
Nếu nhị tiếp tuyến của lối tròn trặn hạn chế nhau bên trên một điểm thì:
- Điểm cơ cơ hội đều nhị tiếp điểm.
- Tia kẻ kể từ điểm cơ trải qua tâm là tia phân giác của những góc tạo nên bởi vì nhị tiếp tuyến.
- Tia kẻ kể từ tâm trải qua điểm này đó là tia phân giác của góc tạo nên bởi vì nhị nửa đường kính trải qua tiếp điểm.
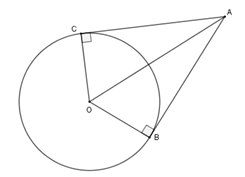
Nghĩa là mang lại lối tròn trặn $\left( O \right)$, $B,C \in \left( O \right)$. Tiếp tuyến của $\left( O \right)$ bên trên $B,C$ hạn chế nhau bên trên $A$.
Khi đó
- $AB = AC$
- Tia $OA$ là phân giác góc $\widehat {BOC}$
- Tia $AO$ là phân giác góc $\widehat {BAC}$
2. Đường tròn trặn nội tiếp tam giác
Đường tròn trặn xúc tiếp với phụ vương cạnh của một tam giác gọi là đường tròn trặn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp lối tròn trặn.
Tâm của lối tròn trặn nội tiếp tam giác là phó của những lối phân giác những góc nhập tam giác.
3. Đường tròn trặn bàng tiếp tam giác
- Đường tròn trặn xúc tiếp với cùng một cạnh của tam giác và xúc tiếp với phần kéo dãn dài của nhị cạnh sót lại gọi là đường tròn trặn bàng tiếp tam giác.
- Tâm của lối tròn trặn bàng tiếp tam giác là phó điểm của một lối phân giác nhập và 2 lối phân giác ngoài của tam giác
- Với một tam giác đem phụ vương lối tròn trặn bàng tiếp.
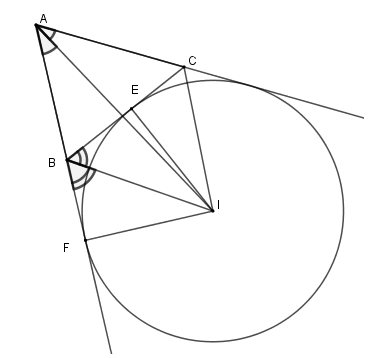
Ví dụ: Xét tam giác $ABC$, tâm của lối tròn trặn bàng tiếp tam giác góc $A$ là phó điểm của hai tuyến đường phân giác ngoài bên trên $B, C$, hoặc là phó điểm của lối phân giác nhập góc $A$ và lối phân giác ngoài bên trên $B$ (hoặc $C$).
Xem thêm: tính từ trong tiếng anh là gì
CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1: Chứng minh những đường thẳng liền mạch tuy nhiên song (vuông góc), chứng tỏ nhị đoạn trực tiếp đều nhau.
Phương pháp:
Dùng đặc thù của nhị tiếp tuyến hạn chế nhau.
Dạng 2: Chứng minh một đường thẳng liền mạch là tiếp tuyến, tính phỏng lâu năm, số đo góc và những nguyên tố không giống.
Phương pháp:
- Dùng khái niệm tiếp tuyến; đặc thù của nhị tiếp tuyến hạn chế nhau.
- Dùng định nghĩa lối tròn trặn nội tiếp, bàng tiếp.
- Dùng hệ thức lượng về cạnh và góc nhập tam giác vuông.
Bình luận
![]() Chia sẻ
Chia sẻ
-
Trả điều thắc mắc 1 Bài 6 trang 113 SGK Toán 9 Tập 1
Giải Trả điều thắc mắc Bài 6 trang 113 SGK Toán 9 Tập 1. Cho hình 79 nhập cơ AB, AC theo đuổi trật tự là những tiếp tuyến bên trên B, bên trên C của lối tròn trặn (O)
-
Trả điều thắc mắc 2 Bài 6 trang 114 SGK Toán 9 Tập 1
Giải Trả điều thắc mắc Bài 6 trang 114 SGK Toán 9 Tập 1. Hãy nêu cơ hội dò xét tâm của một miếng mộc hình trụ bởi vì “thước phân giác”
-
Trả điều thắc mắc 3 Bài 6 trang 114 SGK Toán 9 Tập 1
Giải Trả điều thắc mắc 3 Bài 6 trang 114 SGK Toán 9 Tập 1. Cho tam giác ABC. Gọi I là phó điểm của những lối...
-
Trả điều thắc mắc 4 Bài 6 trang 115 SGK Toán 9 Tập 1
Cho tam giác ABC, K là phó điểm những lối phân giác của nhị góc ngoài bên trên B và C; D, E, F
-
Bài 26 trang 115 SGK Toán 9 tập luyện 1
Giải bài xích 26 trang 115 SGK Toán 9 tập luyện 1. Cho lối tròn trặn (O), điểm A ở bên phía ngoài lối tròn trặn.
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Xem thêm: dấu hiệu nhận biết tứ giác nội tiếp
Tham Gia Group 2K9 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến lớp 9 và luyện nhập lớp 10 bên trên Tuyensinh247.com, khẳng định canh ty học viên lớp 9 học tập chất lượng tốt, trả trả khoản học phí nếu như học tập ko hiệu suất cao.











Bình luận