Chủ đề cho hình chóp s abcd: Hình chóp S.ABCD là 1 trong hình học tập rất đẹp và thú vị. Với lòng là hình vuông vắn và SA vuông góc với lòng, hình chóp này tạo thành một sự bằng vận và khác biệt. Góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD) cũng mang ý nghĩa hóa học đặc trưng và có mức giá trị xứng đáng xem xét. Đây là 1 trong trong mỗi góc nhìn hấp dẫn sự quan hoài của đối tượng người dùng lần lần.
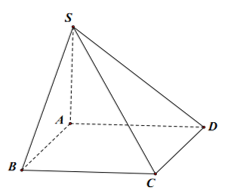
Cho hình chóp S.ABCD đem lòng ABCD là hình vuông vắn cạnh a, SA vuông góc với lòng và SA = a, góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD) vị bao nhiêu?
Để giải việc này, tớ cần thiết vẽ hình và dùng kỹ năng về hình học tập không khí.
Vì hình chóp S.ABCD đem lòng ABCD là hình vuông vắn cạnh a, SA vuông góc với lòng và SA = a, tớ hoàn toàn có thể vẽ hình chóp S.ABCD như sau:
- Vẽ hình vuông vắn ABCD với cạnh a.
- Kẻ SA vuông góc với lòng ABCD và có tính nhiều năm SA = a.
- Nối những điểm S, A, B, C, D sẽ được hình chóp S.ABCD.
Tiếp theo dõi, tất cả chúng ta cần thiết tính góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD).
Gọi M là trung điểm của cạnh CD. Vì lòng ABCD là hình vuông vắn và SA vuông góc với lòng, tớ đem AM vuông góc với CD bên trên M. Do ê, tam giác AMD là tam giác vuông bên trên M.
Vì tam giác AMD là tam giác vuông và SA vuông góc với lòng ABCD, tớ hoàn toàn có thể thấy rằng mặt mày phẳng phiu (SAB) vuông góc với mặt mày phẳng phiu (SCD) bên trên đường thẳng liền mạch AM.
Vì vậy, góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD) đó là góc thân thích hai tuyến đường trực tiếp AM và CD.
Vì cạnh CD là cạnh của lòng ABCD và M là trung điểm của CD, tớ đem CM = MD = 50% * a.
Vì SA = a và tam giác AMD là tam giác vuông bên trên M, tớ đem AM = sqrt(SA^2 - SM^2) = sqrt(a^2 - (1/2 * a)^2) = sqrt(3/4 * a^2) = (sqrt(3)/2) * a.
Vậy tỉ lệ thành phần AM:CD = (sqrt(3)/2) * a : a = sqrt(3)/2 : sqrt(1/2) = (sqrt(3)/2) / (sqrt(2)/2) = sqrt(3)/sqrt(2) = sqrt(6)/2 : sqrt(2)/2 = sqrt(6)/2 * 2/sqrt(2) = sqrt(6).
Vậy góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD) vị góc thân thích đường thẳng liền mạch AM và CD = góc thân thích hai tuyến đường trực tiếp AM và MD = arctan(sqrt(6)) ≈ 1,2490 radian.
Nên góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD) là khoảng tầm 1,2490 radian.
Bạn đang xem: cho hình chóp s abcd

Góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD) vị bao nhiêu?
Để lần góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD) vô hình chóp S.ABCD, tớ cần dùng kỹ năng về Định lý những mặt mày phẳng phiu vuông góc vô không khí và đặc thù của hình chóp đem lòng là hình vuông vắn.
Đầu tiên, tớ xét đường thẳng liền mạch SA và đường thẳng liền mạch SB, cả nhì đều phía trên mặt mày phẳng phiu (SAB). Vì SA vuông góc với lòng ABCD và lòng là hình vuông vắn, tớ hoàn toàn có thể tóm lại rằng SA hạn chế đường thẳng liền mạch SB trở nên nhì đoạn có tính nhiều năm đều nhau.
Tiếp theo dõi, tớ xét đường thẳng liền mạch SC và đường thẳng liền mạch SD, cả nhì đều phía trên mặt mày phẳng phiu (SCD). Lại hoàn toàn có thể vận dụng đặc thù của hình vuông vắn nhằm tóm lại rằng SC hạn chế đường thẳng liền mạch SD trở nên nhì đoạn có tính nhiều năm đều nhau.
Do cả SA và SC đều hạn chế những đường thẳng liền mạch ứng SB và SD trở nên nhì đoạn có tính nhiều năm đều nhau, tớ hoàn toàn có thể suy đi ra rằng góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD) là 1 trong góc vuông (góc 90 độ).
Vậy, góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD) vô hình chóp S.ABCD là 90 chừng.
Đáy của hình chóp S.ABCD là hình gì?
The result of the tìm kiếm indicates that the base of the pyramid S.ABCD is a square (hình vuông).
Cạnh của lòng ABCD có tính nhiều năm bao nhiêu?
Bạn mang đến hình chóp S.ABCD đem lòng ABCD là hình vuông vắn cạnh a và SA vuông góc với lòng và SA = a. Để lần cạnh của lòng ABCD, tớ hoàn toàn có thể vận dụng một trong những cách thức như sau:
1. Sử dụng đặc thù của hình vuông: Vì ABCD là hình vuông vắn nên những cạnh của chính nó đều đều nhau. Vì vậy, cạnh của lòng ABCD cũng vị a.
2. Sử dụng một trong những đặc thù của hình học: Ta hoàn toàn có thể nhận biết rằng hình chóp S.ABCD đem những tam giác đặc trưng, ví dụ như tam giác SAB và tam giác SCD. Ta hoàn toàn có thể vận dụng những công thức tính cạnh của những tam giác này nhằm lần cạnh của lòng ABCD.
3. Chứng minh bằng phương pháp dùng công thức tính thể tích của hình chóp: Thể tích của hình chóp S.ABCD hoàn toàn có thể tính vị công thức V = (1/3) * S * h, vô ê S là diện tích S lòng ABCD và h là độ cao SA. Nếu tớ biết độ quý hiếm của V, S và h, tớ hoàn toàn có thể suy đi ra cạnh của lòng ABCD.
Tóm lại, cạnh của lòng ABCD của hình chóp S.ABCD có tính nhiều năm là a.
Đường cao của hình chóp S.ABCD vị lối cao của hình gì?
Đường cao của hình chóp S.ABCD vị lối cao của hình vuông vắn ABCD.
Để minh chứng điều này, tớ cần thiết minh chứng rằng đường thẳng liền mạch SA hạn chế đường thẳng liền mạch vuông góc với mặt mày phẳng phiu lòng ABCD và trải qua trung điểm của đoạn trực tiếp AB (gọi là hình vuông vắn ABCD).
Ta hiểu được vô hình vuông vắn ABCD, lối cao hạn chế đoạn trực tiếp vuông góc với lòng và trải qua trung điểm của đoạn trực tiếp AB. Đồng thời, đường thẳng liền mạch SA vô hình chóp S.ABCD cũng hạn chế đoạn trực tiếp vuông góc với mặt mày phẳng phiu lòng ABCD và trải qua trung điểm của đoạn trực tiếp AB.
Vì vậy, tớ hoàn toàn có thể tóm lại rằng lối cao của hình chóp S.ABCD vị lối cao của hình vuông vắn ABCD.
_HOOK_
TIẾT 2: HÌNH CHÓP CÓ ĐÁY LÀ HÌNH VUÔNG - ĐT vuông góc MP
Hình chóp vuông góc: quý khách hàng mong muốn tìm hiểu vẻ rất đẹp khác biệt của hình chóp vuông góc? Hãy coi đoạn phim này nhằm làm rõ về những điểm lưu ý đặc trưng của hình học tập này và phương pháp tính toán đầy đủ nhằm tạo nên tuyệt hảo với bè bạn và mái ấm gia đình.
Thể Tích Khối Chóp Toán 12 - Phần 1 | Thầy Nguyễn Phan Tiến
Thể tích khối chóp: quý khách hàng đang được lần hiểu về kiểu cách tính thể tích khối chóp một cơ hội đơn giản dễ dàng và thời gian nhanh chóng? Xem đoạn phim này nhằm làm rõ về công thức tính và cơ hội phần mềm nó vô những việc thực tiễn. Hãy sẵn sàng nhằm phát triển thành Chuyên Viên trong công việc đo lường và tính toán thể tích khối chóp!
Tỉ số thể tích thân thích nhì khối chóp S.A\'B\'C\'D\' và S.ABCD là bao nhiêu?
Để tính tỉ số thể tích thân thích nhì khối chóp S.A\'B\'C\'D\' và S.ABCD, tớ nên biết về mối quan hệ Một trong những độ cao thấp của nhì khối chóp này.
Ở trên đây, tớ đem nhì khối chóp:
- Chóp S.ABCD đem lòng ABCD là hình vuông vắn cạnh a, và SA vuông góc với lòng và có tính nhiều năm vị a.
- Chóp S.A\'B\'C\'D\' đem lòng A\'B\'C\'D\' cũng chính là hình vuông vắn cạnh a, và những đỉnh A\', B\', C\', D\' theo thứ tự là trung điểm của SA, SB, SC, SD.
Để tính tỉ số thể tích thân thích nhì khối chóp này, tớ tiếp tục người sử dụng quy tắc tỉ số thể tích của nhì khối hình tồn bên trên mối quan hệ tỷ trọng với cạnh cộng đồng hoặc diện tích S địa thế căn cứ của bọn chúng.
Quan sát tớ thấy rằng, trong những khối chóp, những cạnh đối xứng qua quýt trục ở trong lòng đều phải sở hữu chừng nhiều năm đều nhau (vì A\', B\', C\', D\' theo thứ tự là trung điểm của SA, S
Gọi A\', B\', C\', D\' là gì vô hình chóp S.ABCD?
Trong hình chóp S.ABCD, tớ gọi A\', B\', C\', D\' theo thứ tự là trung điểm của những đỉnh A, B, C, D.
Xem thêm: trường đại học văn hoá tp hcm
Cách tính tỉ số thể tích của nhì khối chóp S.A\'B\'C\'D\' và S.ABCD?
Để tính tỉ số thể tích của nhì khối chóp S.A\'B\'C\'D\' và S.ABCD, tớ nên biết rõ rệt về điểm lưu ý của nhì khối chóp này.
Khối chóp S.ABCD là 1 trong khối chóp đem lòng là hình vuông vắn ABCD đem cạnh là a và SA vuông góc với lòng và có tính nhiều năm vị a.
Khối chóp S.A\'B\'C\'D\' là 1 trong khối chóp đem lòng là tứ giác A\'B\'C\'D\' được tạo nên trở nên từ các việc lấy những trung điểm A\', B\', C\', D\' của những cạnh SA, SB, SC, SD của khối chóp S.ABCD.
Để tính tỉ số thể tích của nhì khối chóp này, tớ dùng công thức:
Tỉ số thể tích = (thể tích khối chóp S.A\'B\'C\'D\') / (thể tích khối chóp S.ABCD)
Công thức tính thể tích của một khối chóp là:
Thể tích khối chóp = (diện tích đáy) x (chiều cao) / 3
Đầu tiên, tớ cần thiết tính diện tích S lòng của khối chóp S.ABCD. Vì lòng là hình vuông vắn đem cạnh a, nên diện tích S lòng là a^2.
Tiếp theo dõi, tớ cần thiết tính độ cao của khối chóp S.ABCD. Vì SA vuông góc với lòng và có tính nhiều năm vị a, nên độ cao của khối chóp cũng vị a.
Áp dụng công thức tính thể tích của khối chóp S.ABCD, tớ có:
Thể tích khối chóp S.ABCD = (a^2) x a / 3 = a^3 / 3
Tiếp theo dõi, tớ cần thiết tính diện tích S lòng của khối chóp S.A\'B\'C\'D\'. Vì lòng là tứ giác A\'B\'C\'D\' được tạo nên trở nên từ các việc lấy những trung điểm của những cạnh SA, SB, SC, SD của khối chóp S.ABCD, nên diện tích S lòng của khối chóp S.A\'B\'C\'D\' cũng chính là a^2.
Cuối nằm trong, tớ cần thiết tính độ cao của khối chóp S.A\'B\'C\'D\'. Ta thấy rằng khối chóp S.A\'B\'C\'D\' tương tự với 1 khối chóp S.ABCD, bởi vậy độ cao của khối chóp S.A\'B\'C\'D\' cũng vị a.
Áp dụng công thức tính thể tích của khối chóp S.A\'B\'C\'D\', tớ có:
Thể tích khối chóp S.A\'B\'C\'D\' = (a^2) x a / 3 = a^3 / 3
Cuối nằm trong, tớ tính tỉ số thể tích của nhì khối chóp:
Tỉ số thể tích = (a^3 / 3) / (a^3 / 3) = 1
Vậy tỉ số thể tích của nhì khối chóp S.A\'B\'C\'D\' và S.ABCD vị 1.
Gọi M là trung điểm của SC, lần kí thác điểm I của AM và (SBD)?
Để lần kí thác điểm I của AM và mặt mày phẳng phiu (SBD), tớ tiếp tục dùng kí thác điểm của hai tuyến đường trực tiếp nhằm lần đi ra I.
Đầu tiên, tớ cần thiết lần tọa chừng của điểm M. Gọi S là 1 trong điểm đem tọa chừng (xS, yS, zS), A đem tọa chừng (xA, yA, zA), và C đem tọa chừng (xC, yC, zC). Do M là trung điểm của SC, tớ hoàn toàn có thể tính được tọa chừng của M bằng phương pháp lấy tầm nằm trong của tọa chừng của S và C:
xM = (xS + xC) / 2
yM = (yS + yC) / 2
zM = (zS + zC) / 2
Sau khi đã có được tọa chừng của điểm M, tớ hoàn toàn có thể dẫn đến một vector trải qua 2 điểm A và M bằng phương pháp trừ tọa chừng của M mang đến tọa chừng của A:
AM = (xM - xA, yM - yA, zM - zA)
Tiếp theo dõi, tớ cần thiết xác lập phương trình mặt mày phẳng phiu (SBD). Gọi ABCD là hình chữ nhật đem lòng và S là đỉnh của hình chóp. Vì S là đỉnh của hình chóp, nên tớ hiểu được vector thỏa mãn nhu cầu SAB vuông góc với vector thỏa mãn nhu cầu SCD. Ta hoàn toàn có thể dẫn đến vector thỏa mãn nhu cầu SAB bằng phương pháp trừ tọa chừng của A mang đến tọa chừng của S:
AS = (xA - xS, yA - yS, zA - zS)
Tương tự động vì vậy, tớ hoàn toàn có thể dẫn đến vector thỏa mãn nhu cầu SCD bằng phương pháp trừ tọa chừng của C mang đến tọa chừng của S:
CS = (xC - xS, yC - yS, zC - zS)
Sau khi đã có được nhì vector AS và CS, tớ hoàn toàn có thể lần vector pháp tuyến của mặt mày phẳng phiu (SBD) bằng phương pháp tích vô vị trí hướng của nhì vector này:
n = AS x CS
Ở trên đây, \"x\" thay mặt đại diện được chấp nhận nhân vector. Vậy vector pháp tuyến của mặt mày phẳng phiu (SBD) là n.
Cuối nằm trong, nhằm lần kí thác điểm I của đường thẳng liền mạch AM và mặt mày phẳng phiu (SBD), tớ tiếp tục triển khai công việc sau:
1. Xác quyết định phương trình đường thẳng liền mạch AM bằng phương pháp dùng điểm A và vector AM:
Đường trực tiếp AM: x = xA + t * (xM - xA)
y = yA + t * (yM - yA)
z = zA + t * (zM - zA)
2. Thay những phương trình x, hắn, z của đường thẳng liền mạch AM vô phương trình mặt mày phẳng phiu (SBD) (xS - xB)(x - xS) + (yS - yB)(y - yS) + (zS - zB)(z - zS) = 0 nhằm lần kí thác điểm I.
3. Giải phương trình vừa phải dẫn đến nhằm lần tọa chừng của kí thác điểm I.
Chứng minh rằng IA = 2IM vô hình chóp S.ABCD.
Để minh chứng rằng IA = 2IM vô hình chóp S.ABCD, tất cả chúng ta hoàn toàn có thể dùng cách thức dùng hình phức tạp.
Bước 1: Vẽ lối chéo cánh AC của hình vuông vắn ABCD và vẽ đường thẳng liền mạch AM.
Bước 2: Chứng minh rằng TAMB là hình bình hành. Ta hoàn toàn có thể dùng những mệnh đề về góc vô hình bình hành nhằm minh chứng điều này.
Bước 3: Chứng minh rằng TAM và SAB là nhì tam giác đồng dạng. phẳng cơ hội dùng đặc thù của những cặp góc đồng dạng, tất cả chúng ta hoàn toàn có thể minh chứng rằng TAM và SAB là nhì tam giác đồng dạng.
Bước 4: Vì TAM và SAB là nhì tam giác đồng dạng, tớ hoàn toàn có thể dùng tỷ trọng thân thích cạnh và lối cao vô nhì tam giác đồng dạng nhằm minh chứng rằng IA = 2IM. Cụ thể, tớ có:
IA/AM = SA/AB
2IM/AM = SC/AB
Bước 5: Từ những phương trình ở bước trước, tất cả chúng ta hoàn toàn có thể thấy rằng IA = 2IM.
Vậy tất cả chúng ta tiếp tục minh chứng được rằng IA = 2IM vô hình chóp S.ABCD.
_HOOK_
Thiết Diện Của Hình Chóp - Toán 11 | Thầy Nguyễn Phan Tiến
Thiết diện hình chóp: Hình chóp và tiết diện của chính nó luôn luôn mang về những quan hoài đặc trưng vô hình học tập. Hãy tìm hiểu những kín đáo về tiết diện của hình chóp và cơ hội tiếp cận yếu tố này trải qua đoạn phim thú vị này. Sẽ cực kỳ thú vị khi chúng ta hiểu thâm thúy rộng lớn về cấu tạo và đặc thù của hình chóp.
Tìm kí thác điểm I của AM và (SBD) vô hình chóp S.ABCD.
Để lần kí thác điểm I của AM và (SBD) vô hình chóp S.ABCD, tất cả chúng ta hoàn toàn có thể vận dụng nhì cách thức sau:
Phương pháp 1:
1. Vẽ đường thẳng liền mạch AM trải qua trung điểm M của cạnh SC.
2. Vẽ đường thẳng liền mạch BD.
3. Gọi I là kí thác điểm của đường thẳng liền mạch AM và đường thẳng liền mạch BD.
4. Kết trái khoáy là đường thẳng liền mạch AI.
Phương pháp 2:
1. Gọi N là kí thác điểm của đường thẳng liền mạch SC và mặt mày phẳng phiu (ABCD).
2. Gọi I là kí thác điểm của đường thẳng liền mạch AN và đường thẳng liền mạch BD.
3. Kết trái khoáy là đường thẳng liền mạch AI.
Lưu ý: Điều khiếu nại quan trọng mang đến phần vấn đáp này là hình chóp S.ABCD được nghĩ rằng hình bình hành.
Gọi M là trung điểm của SC, thì góc thân thích MA và MC vị bao nhiêu?
Ta có:
- Góc thân thích nhì mặt mày phẳng phiu (SAB) và (SCD) vị 90 chừng (trong tế bào miêu tả của câu 1).
- Gọi M là trung điểm của SC (theo câu 3).
- Vì M là trung điểm của SC nên SM = MC (kẻ đường thẳng liền mạch ST qua quýt M tuy vậy song với AB, với T là tiếp điểm của ST và (ABCD)).
- Vì góc thân thích hai tuyến đường trực tiếp tuy vậy song và nằm trong hạn chế một lối chéo cánh là góc vuông nên góc thân thích MA và MC cũng vị 90 chừng.
=> Góc thân thích MA và MC vị 90 chừng.
Góc thân thích nhì mặt mày phẳng phiu (SBD) và (SAB) vô hình chóp S.ABCD là bao nhiêu?
Góc thân thích nhì mặt mày phẳng phiu (SBD) và (SAB) vô hình chóp S.ABCD hoàn toàn có thể tính vị công thức sau:
Gọi O là trung điểm của đoạn SA.
Ta đem nhì vectơ SB và SD. Góc thân thích nhì mặt mày phẳng phiu (SBD) và (SAB) tiếp tục vị góc thân thích nhì vectơ này. Ta đem công thức tính góc thân thích nhì vectơ vô không khí tía chiều như sau:
cos(θ) = (SB • SD) / (|SB| • |SD|)
Trong ê, SB • SD là tích vô vị trí hướng của nhì vectơ SB và SD, |SB| và |SD| theo thứ tự là chừng nhiều năm của nhì vectơ SB và SD.
Để đo lường và tính toán công thức bên trên, tớ nên biết những thông số kỹ thuật không giống vô hình chóp S.ABCD như chừng nhiều năm cạnh của lòng ABCD, địa điểm của điểm A và tài liệu về góc thân thích nhì vectơ SB và SD.
Dựa bên trên những vấn đề và công thức tính góc thân thích nhì vectơ bên trên, tớ hoàn toàn có thể tính được góc thân thích nhì mặt mày phẳng phiu (SBD) và (SAB) vô hình chóp S.ABCD.
Xem thêm: cho dạng đúng của từ trong ngoặc
Gọi A\' là trung điểm của SA, thì góc thân thích SC và A\'C\' vị bao nhiêu?
Để lần góc thân thích SC và A\'C\', tớ tiếp tục xét tam giác vuông SC\'A\'. Gọi M là trung điểm của SA. Khi ê, tớ có:
- Góc thân thích nhì mặt mày phẳng phiu (SC\'A\') và (SCA\') vị góc thân thích hai tuyến đường trực tiếp SC và A\'C\'.
- Góc thân thích nhì mặt mày phẳng phiu (SCA\') và (SCA) vị góc thân thích hai tuyến đường trực tiếp SC và SA (vì A\' là trung điểm của SA).
- Góc thân thích nhì mặt mày phẳng phiu (SCA) và (SAB) vị 90 chừng (do SA vuông góc với lòng ABCD).
Vậy, nhằm lần góc thân thích SC và A\'C\', tớ chỉ việc lần góc thân thích nhì mặt mày phẳng phiu (SCA\') và (SAB).
Từ thắc mắc, tớ hiểu được lòng ABCD là hình vuông vắn, nên góc thân thích SAB và SCD vị 45 chừng.
Khi ê, góc thân thích nhì mặt mày phẳng phiu (SCA\') và (SAB) tiếp tục vị 45 chừng.
Vậy, góc thân thích SC và A\'C\' là 45 chừng.
Tìm kí thác điểm của A\'C\' và (SAB) vô hình chóp S.ABCD.
Để lần kí thác điểm của A\'C\' và (SAB) vô hình chóp S.ABCD, tớ cần thiết lần tọa chừng của điểm A\' và tương tự với tọa chừng của những đỉnh A, B, C, D.
Giả sử tọa chừng của đỉnh A là (0, 0, 0), được lựa chọn là gốc O. Mặt không giống đỉnh B đem tọa chừng (a, 0, 0), C đem tọa chừng (a, a, 0) và D đem tọa chừng (0, a, 0).
Vì A\' là trung điểm của SA, tớ đem tọa chừng của A\' là (a/2, a/2, a/2).
Để lần kí thác điểm của A\'C\' và (SAB), tớ cần thiết lần phương trình mặt mày phẳng phiu trải qua 3 điểm A\', B, A.
Ta màn biểu diễn điểm A\' là A\' = (x, hắn, z).
- Điểm B đem tọa chừng B = (a, 0, 0) = B = (a - x, -y, -z).
- Điểm A đem tọa chừng A = (0, 0, 0) = A = (-x, -y, -z).
Để lần phương trình mặt mày phẳng phiu (SAB), tớ dùng công thức phương trình mặt mày phẳng phiu trải qua 3 điểm:
Ax + By + Cz + D = 0
Thay thế vị những tọa chừng của 3 điểm A, B, A\' mang đến phương trình mặt mày phẳng phiu (SAB), tớ có:
(-x)x + (-y)y + (-z)z + D = 0
-x^2 - y^2 - z^2 + D = 0
Với điểm A\' đem tọa chừng (a/2, a/2, a/2), tớ thay cho thế vô phương trình trên:
-((a/2)^2) - ((a/2)^2) - ((a/2)^2) + D = 0
Simplifying the equation, we get:
-a^2/4 - a^2/4 - a^2/4 + D = 0
-3a^2/4 + D = 0
D = 3a^2/4
Phương trình mặt mày phẳng phiu (SAB) là: -x^2 - y^2 - z^2 + 3a^2/4 = 0.
Tiếp theo dõi, nhằm lần kí thác điểm của A\'C\' và (SAB), tớ thay cho tọa chừng của A\' vô phương trình mặt mày phẳng phiu (SAB):
-((a/2)^2) - ((a/2)^2) - ((a/2)^2) + 3a^2/4 = 0.
Simplifying the equation, we get:
-a^2/4 - a^2/4 - a^2/4 + 3a^2/4 = 0
-a^2/4 = 0
a^2 = 0.
The equation tells us that a must be equal to tướng 0, which means that the points A\'B\'C\'D\' degenerate into a single point and A\'C\' is coincident with (SAB).
Tóm lại, nhằm lần kí thác điểm của A\'C\' và (SAB) vô hình chóp S.ABCD, tớ thấy rằng những điểm A\'B\'C\'D\' đều trùng nhau và A\'C\' trùng với (SAB) khi a = 0.
_HOOK_












Bình luận