chu vi hình tứ giác

Công thức tính chu vi hình tứ giác như làm sao? Vốn dĩ hình học tập đem thật nhiều biến hóa thể không giống nhau nên công thức tính của đặc biệt nhiều mẫu mã. Chính bởi vậy, nhằm mục đích mục tiêu giúp đỡ bạn hiểu nắm rõ rộng lớn về lý thuyết tính chu vi, tương tự hoàn toàn có thể vận dụng được công thức vô thực tiễn. Ngay tiếp sau đây Hoàng Hà Mobile đang được tổ hợp cho mình những vấn đề cần thiết nhất, đem bao hàm bài bác thói quen chu vi và điều giải. Mời các bạn nằm trong liếc qua và nâng lên kiến thức và kỹ năng với Cửa Hàng chúng tôi nhé.

Một hình tứ giác đơn giản và giản dị là một trong hình đem tứ đỉnh, tứ cạnh và tứ góc. Tuy nhiên, có không ít Đặc điểm và loại không giống nhau của hình tứ giác, tạo ra sự nhiều mẫu mã trong số công thức toán học tập. Các mô hình tứ giác phổ cập bao hàm hình vuông vắn, hình chữ nhật, hình thang và hình bình hành. 

Bạn đang xem: chu vi hình tứ giác

Theo cơ, từng mô hình tứ giác đem theo đuổi những tính chất riêng lẻ và quy luật về góc, cạnh tương tự đối xứng. Đồng thời, so với hình tứ giác nào là, tỉ lệ thành phần những cạnh và góc hoàn toàn có thể thay cho thay đổi, đưa đến những hình dạng và đặc điểm không giống nhau. điều đặc biệt, vô toán học tập, hình tứ giác thông thường được nghiên cứu và phân tích sâu sắc rộng lớn vô nghành nghề dịch vụ hình học tập bằng và không khí. 

Tại sao công thức tính chu vi hình tứ giác lại quan tiền trọng?

Chu vi là một trong đại lượng tính toán chiều lâu năm, và nó canh ty tế bào mô tả độ cao thấp tổng thể của hình tứ giác. Như vậy thiệt sự hữu dụng Lúc người tiêu dùng mong muốn hiểu tương tự đo lường những quy mô vô không khí. Dường như, chu vi còn hỗ trợ phân loại những mô hình tứ giác và thực hiện nổi trội những đặc điểm đặc trưng của bọn chúng. Từ cơ, tất cả chúng ta hoàn toàn có thể coi đấy là một dụng cụ quan trọng nhằm hiểu ra rộng lớn về tính chất của những hình trạng học tập đang được tồn bên trên xung xung quanh tất cả chúng ta.

Hơn thế nữa, công thức tính chu vi của những hình tứ giác không những được vận dụng vô dạy dỗ học viên. Mà ở thực tiễn biệt, phương pháp tính chu vi được dùng rộng thoải mái trong số nghành nghề dịch vụ như phong cách thiết kế, kiến thiết và công nghiệp. Để kể từ cơ canh ty người tiêu dùng hoàn toàn có thể đo lường lượng vật tư quan trọng hoặc nhằm đáp ứng chừng chắc chắn rằng của những kết cấu vô dự án công trình.

Công thức tính chu vi hình tứ giác như vậy nào?

Ở phần định nghĩa, Cửa Hàng chúng tôi cũng đều có nhắc tới nhiều mẫu mã không giống nhau của hình tứ giác. Tuy nhiên, nhằm mục đích canh ty cho mình hiểu đơn giản dễ dàng vận dụng công thức hơn vậy thì Cửa Hàng chúng tôi phân thành 2 mô hình tứ giác. Dựa vô phía trên, tất cả chúng ta sẽ sở hữu những công thức vận dụng riêng rẽ và mời mọc các bạn nằm trong tìm hiểu thêm tăng nhé.

Tứ giác bình thường

Chúng tao sẽ sở hữu một công thức cộng đồng nhằm tính chu vi của những hình tứ giác giản đơn. Cụ thể, các bạn sẽ tính chu vi vày tổng chiều lâu năm của những cạnh tứ giác. Ví dụ nếu như một tứ giác đem 4 cạnh là a, b, c và d thì công thức của công ty vày (a + b + c + d).

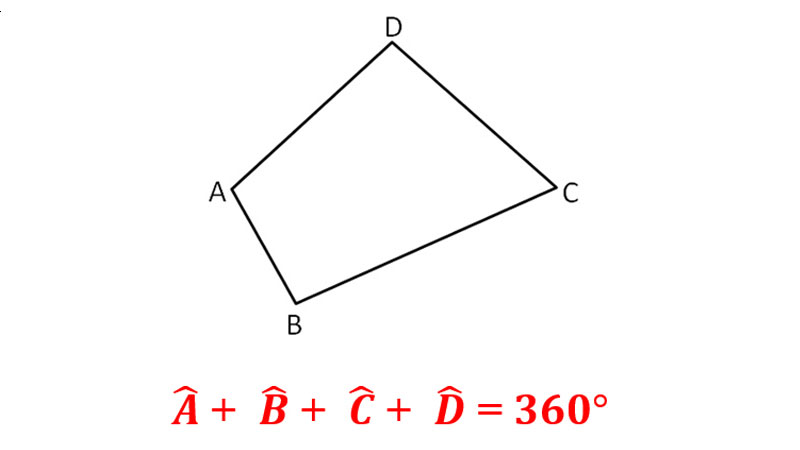
Người sử dụng cần thiết chú ý rằng, công thức này tiếp tục vận dụng với đa số những hình tứ giác, bao hàm cả những hình đem hay là không những cạnh đều bằng nhau. Hay phát biểu theo phía không giống, công thức này hoàn toàn có thể vận dụng đối với tất cả hình chữ nhật, hình vuông vắn và những hình đem tứ cạnh không giống. Và người tiêu dùng chỉ cần phải biết cho tới chừng lâu năm của tứ cạnh là hoàn toàn có thể vận dụng công thức thành công xuất sắc rồi nhé.

Tứ giác đem điều kiện

Đúng theo đuổi tên thường gọi, tứ giác đem ĐK sẽ tiến hành tạo ra trở thành Lúc tùy thuộc vào một vài tiêu chuẩn chắc chắn. Chẳng hạn như tất cả chúng ta sẽ sở hữu một vài quy mô tứ giác vuông, tứ giác cân nặng, tứ giác lồi hoặc tứ giác lõm. Và tùy nằm trong vô đặc điểm của từng hình nhưng mà tất cả chúng ta tiếp tục vận dụng những công thức nhiều mẫu mã như tại đây.

Công thức 1: Chu vi hình tứ giác theo hình thức bình hành: Chu vi (P) = 2 x (Độ lâu năm cạnh lòng + Độ lâu năm cạnh bên).

Công thức 2: Chu vi hình đều (hình tứ giác đem cả tứ cạnh vày nhau): Chu vi (P) = 4 x Độ lâu năm cạnh (a).

Công thức 3: Chu vi hình vuông: Chu vi (P) = 4 x Độ lâu năm cạnh (a).

Công thức 4: Chu vi hình chữ nhật: Chu vi (P) = 2 x (Chiều lâu năm + Chiều rộng) hoặc  Phường = 2a + 2b (nếu a và b là chiều lâu năm và chiều rộng).

Tổng hợp ý những dạng bài bác thói quen chu vi hình tứ giác, đem bài bác giải

“Học nên song song với hành”, Lúc tất cả chúng ta đang được hiểu rằng toàn bộ công thức thì trọng trách tiếp theo sau của công ty là nên vận dụng được nó vô thực tiễn biệt. Hiểu được yếu tố cần thiết này nên ngay lập tức vô phía trên Hoàng Hà Mobile đang được tổ hợp cho mình những dạng bài bác thói quen chu vi hình học tập đặc biệt thú vị. Nếu các bạn bỏ qua qua quýt thì chắc chắn rằng tiếp tục thiếu thốn sót rất rộng đấy nhé.

Dạng 1: Tính chu vi Lúc đang được hiểu rằng chừng lâu năm của những cạnh

Đầu tiên tất cả chúng ta tiếp tục bên nhau lần hiểu dạng bài bác tập luyện cơ phiên bản nhất vô phương pháp tính chu vi hình học tập. Cụ thể, tất cả chúng ta sẽ sở hữu toàn bộ những dữ khiếu nại về chừng lâu năm những cạnh của hình tứ giác. Vậy nên tất cả chúng ta chỉ việc vận dụng công thức Phường = a + b + c + d là hoàn toàn có thể hoàn thiện được thách thức thứ nhất rồi nè.

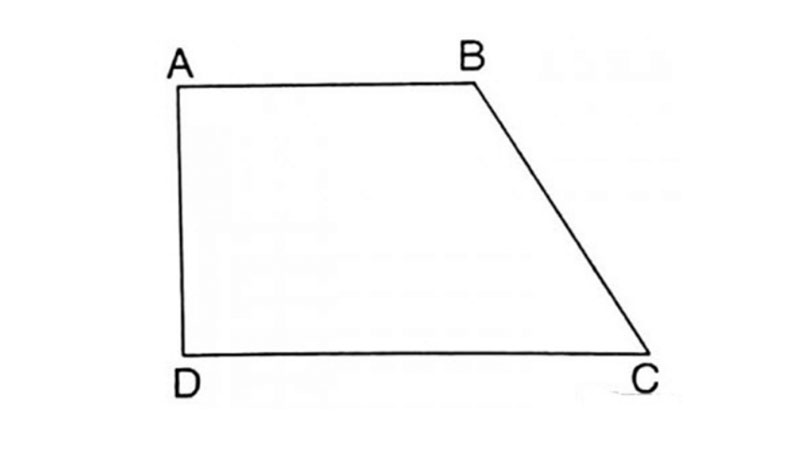
Ví dụ: Chúng tao đã có được chừng lâu năm tứ cạnh, a = 2cm, b = 4cm, c = 6cm và d = 8cm. Dựa vô công thức tính chu vi hình tứ giác, tao có: Phường =  2 + 4 + 6 + 8 = 20cm.

Dạng 2: Có chu vi, tính ngược lại chừng lâu năm những cạnh

Thay vì thế tất cả chúng ta đo lường theo đuổi công thức thuận chiều, với dạng này tất cả chúng ta tiếp tục cút ngược lại một chút ít. Tại phía trên, các bạn sẽ hiểu rằng chu vi của hình tứ giác và đòi hỏi nên tính được chừng lâu năm cạnh. Và tương tự động tất cả chúng ta tiếp tục kế tiếp áp dụng công thức Phường = a + b + c + d ở dạng vấn đề này nhé.

Ví dụ: Chúng tao đem chu vi hình ABCD = AB + BC + CD + DA = 52cm. Đồng thời, tất cả chúng ta cũng hiểu rằng chừng lâu năm nhị cạnh AB + BC = 21cm. Yêu cầu đề ra là các bạn nên tính được tổng chừng lâu năm của nhị cạnh CD + DA.

Xem thêm: lời bài hát em gái mưa

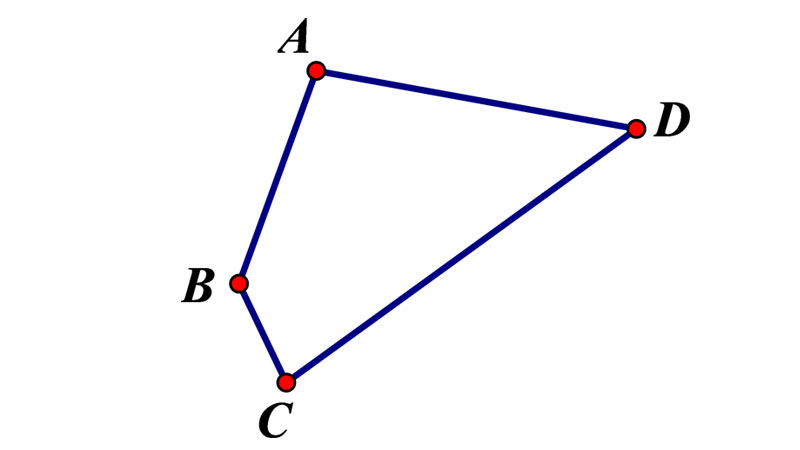
Bài giải: AB + BC = 2P = 21 + (CD + DA) = 45cm. Vậy nhằm giải được vấn đề này tất cả chúng ta tiếp tục triển khai như vậy nào? Trước tiên bạn phải vận dụng công thức và tất cả chúng ta sẽ sở hữu được tổng chừng lâu năm của những cạnh CD + DA = 52 – 21 = 31cm. Vậy là thành phẩm sau cuối của bài bác toàn là 31cm.

Dạng 3: Công thức tính chu vi hình tứ giác đặc biệt

Như đang được biết, tất cả chúng ta sẽ sở hữu hình tứ giác đặc trưng được tạo ra trở thành kể từ những ĐK chắc chắn. Đồng thời, Hoàng Hà Mobile đã và đang cung ứng công thức cụ thể cho mình. Do cơ, ở dạng bài bác tập luyện này tất cả chúng ta sẽ tiến hành cho 1 hình vuông vắn hoặc hình chữ nhật với những dữ khiếu nại về cạnh và đòi hỏi tính chu vi. 

Ví dụ: Mảnh khu đất nhà của bạn hình chữ nhật với chiều lâu năm là 20m và chiều rộng lớn là 8m. Đề bài bác đòi hỏi các bạn nên tính được chu vi của mảnh đất nền bên trên. Từ dữ khiếu nại này, tất cả chúng ta tiếp tục sử dụng công thức Chu vi (P) = 2 x (Chiều lâu năm + Chiều rộng) =  2 x (20 + 8) = 56m.

Bài rèn luyện phương pháp tính chu vi tứ giác giành riêng cho nhỏ bé lớp 3, lớp 4

Bên cạnh việc cung ứng cho tới vấn đề về những dạng bài bác tập luyện phổ cập nhất của hình tứ giác. Hoàng Hà Mobile tiếp tục khêu ý thêm 1 vài ba bài bác rèn luyện nhằm nâng lên kỹ năng đo lường của chúng ta nhỏ. điều đặc biệt bài bác tập luyện này tiếp tục thường xuyên giành riêng cho những nhỏ bé lớp 3 và lớp 4, nên ba mẹ hoàn toàn có thể lần hiểu và nằm trong nhỏ bé giải toán tận nơi nhé.

Bài tập luyện 1

Bác Hải mong muốn lát gạch men cho tới nền buồng nghỉ với chiều lâu năm là 4m và chiều ngang là 3m. Trong số đó, loại gạch men lát nhưng mà chưng dùng đem hình vuông vắn với cạnh là 60cm. Hỏi chưng Hải nên mua sắm từng nào viên gạch men nhằm kiến thiết dứt cho tới phòng ngủ.

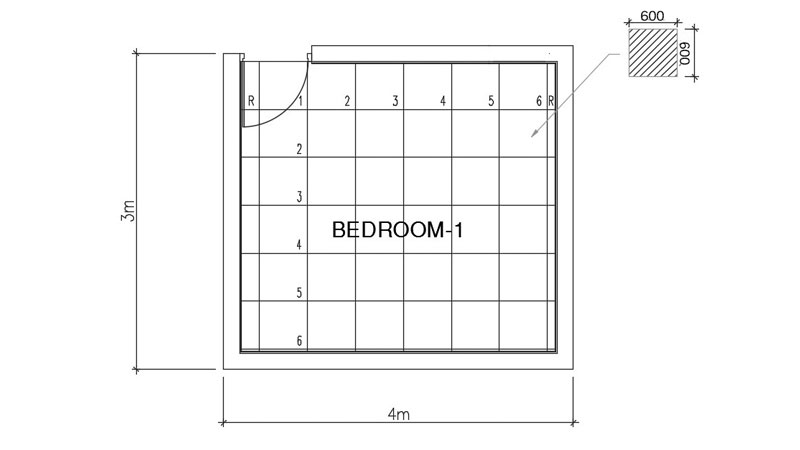
Lời giải: Chúng tao đem diện tích S căn chống vày 4 x 3 = 18m2 = 120.000cm2. Trong số đó, một vuông gạch men sẽ sở hữu diện tích S vày 60 x 60 = 1.200cm2. Vậy tất cả chúng ta sẽ sở hữu tổng số viên gạch men nhưng mà chưng Hải cần dùng là 120.000 : 1.200 = 100 viên.

Bài tập luyện 2

Một hình thoi ABCD có tính lâu năm hai tuyến phố chéo cánh theo lần lượt là 5m và 4m. Vây diện tích S hình thoi ABCD vày bao nhiêu?

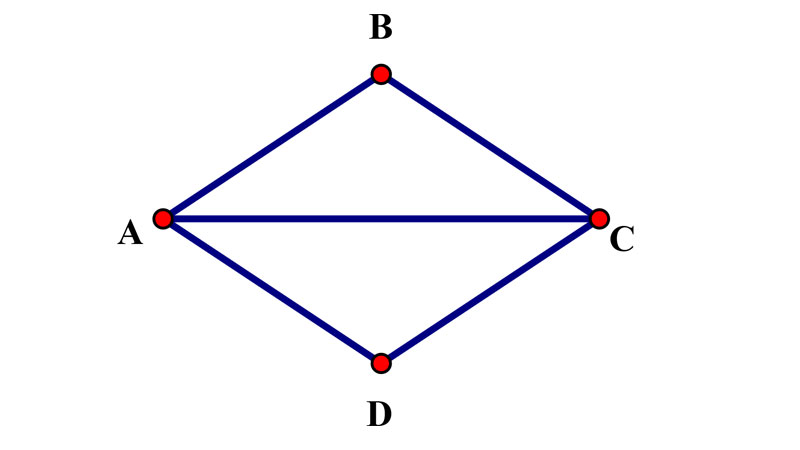
Lời giải: Để tính được vấn đề này nên phát biểu là khôn xiết đơn giản và giản dị, tất cả chúng ta tiếp tục tính diện tích S hình thoi ABCD = (5 x 4)/2 = 10m2. Và thành phẩm sau cuối tất cả chúng ta chiếm được về diện tích S của hình thôi ABCD là 10m2.

Bài tập luyện 3

Một quần thể vườn trồng hoa hình chữ nhật đem chiều lâu năm (a = 15cm) và chiều rộng lớn (b = 10cm). Trong Lúc cơ, cổng đem chiều rộng lớn vày ⅓ chiều lâu năm và phần còn sót lại là sản phẩm rào. Câu chất vấn đề ra là sản phẩm rào của quần thể vườn trồng hoa lâu năm từng nào mét?

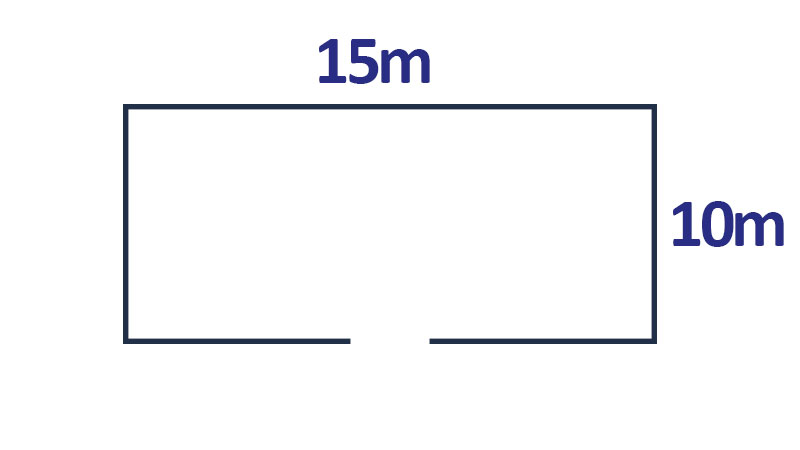
Lời giải: Trước tiên, tất cả chúng ta cần được tính được phạm vi của cổng = 15/3 = 5cm. Tiếp cho tới, các bạn sẽ tính chu vi hình tứ giác (hình chữ nhật) = 2.(10 + 15) = 2.25 = 50m. Vậy tất cả chúng ta hoàn toàn có thể Kết luận rằng chiều lâu năm của sản phẩm rào quần thể vườn trồng hoa vày 50 – 5 = 45m.

Tại sao chu vi tứ giác tiếp tục dựa vào nhiều vô những lối chéo?

Theo vấn đề Cửa Hàng chúng tôi lần hiểu rõ thì đem thật nhiều các bạn vướng mắc rằng “Tại sao hình tứ giác hoàn toàn có thể không giống nhau so với 2 lối chéo cánh không giống nhau?”. Trước hết, độc giả cần phải biết rõ rệt về cấu tạo của hai tuyến phố chéo cánh vô hình học tập tứ giác, cơ đó là 2 lối được tạo ra trở thành Lúc nối những điểm đối xứng, ko ngay tắp lự kề. Song tuy vậy cơ, Lúc tất cả chúng ta tính chu vi của hình tứ giác thì cần phải tính được tổng của những cạnh vô hình.

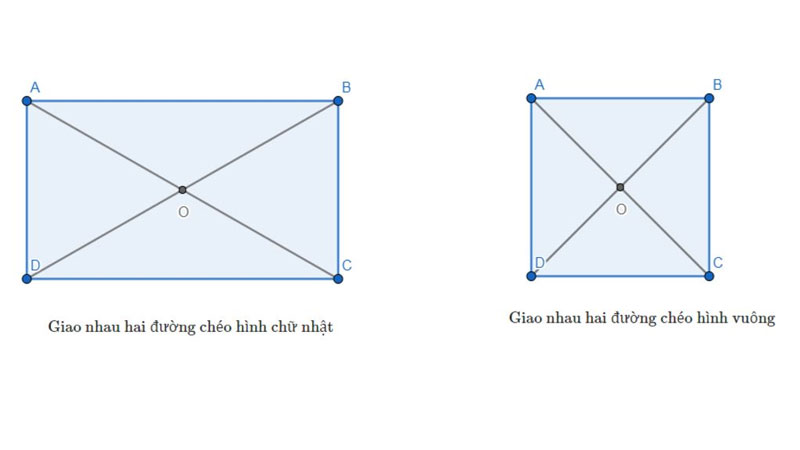
Chính bởi vậy nhưng mà, một Lúc những lối chéo cánh thay cho thay đổi thì chiều lâu năm của những cạnh cũng thay cho thay đổi hợp lý. Kéo Từ đó là tổng của những cạnh cũng thay cho thay đổi và đưa đến một hình tứ giác có không ít biến hóa thể không giống nhau. Ví dụ tất cả chúng ta chọn 1 lối chéo cánh ngắn lại thì tổng chiều lâu năm của những cạnh tiếp tục hạ xuống. Và thành phẩm là chu vi của tứ giác tiếp tục nhỏ rộng lớn đối với việc dùng lối chéo cánh dài thêm hơn.

Xem thêm: dấu hiệu chia hết cho 6

Tuy nhiên mang trong mình một chú ý trọng điểm nhưng mà bạn phải nắm vững, cơ đó là độ cao thấp của lối chéo cánh cũng hoàn toàn có thể tùy thuộc vào loại tứ giác và những đỉnh của chính nó. Chính vì vậy, Lúc tính chu vi tứ giác phụ thuộc những lối chéo cánh thì bạn phải xác lập đúng đắn chừng lâu năm của chính nó để sở hữu được thành phẩm chính nhất.

Kết luận

Như vậy, tất cả chúng ta đang được lần hiểu về cách tính chu vi hình tứ giác là gì. Đồng thời, độc giả cũng biết phương pháp áp dụng công thức vô những vấn đề thực tiễn. Riêng so với chúng ta nhỏ cần được tóm kiên cố những kiến thức và kỹ năng cơ phiên bản này nhằm hỗ trợ cho tới phần đo lường hình học tập ở những lớp bên trên.

Xem thêm:

• Công thức tính tổng sản phẩm số cơ hội đều và sản phẩm số ko cơ hội đều đúng đắn nhất
• Công thức tính nhanh chóng thể tích khối chóp – Tính toán đơn giản dễ dàng và hiệu quả