Phương trình số 1 nhị ẩn x, nó là hệ thức dạng:
1. Các kỹ năng cần thiết nhớ
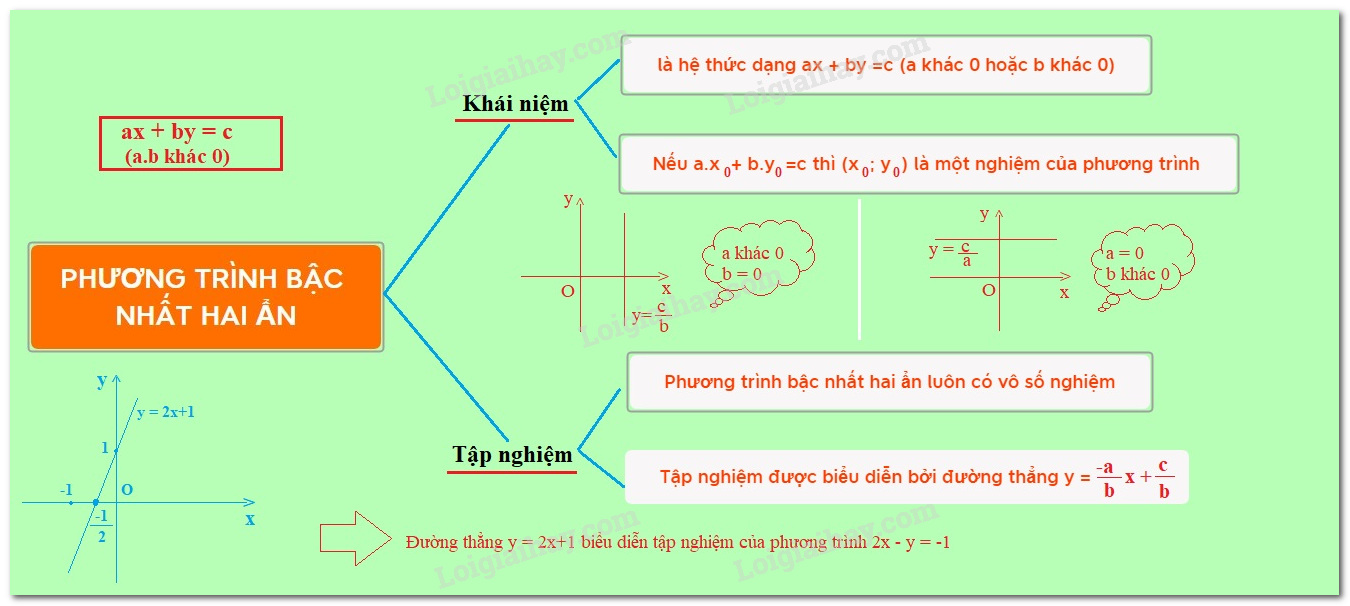
Khái niệm phương trình số 1 nhị ẩn
Bạn đang xem: phương trình bậc nhất 2 ẩn
Quảng cáo
+) Phương trình số 1 nhị ẩn là phương trình với dạng $ax + by = c$
Trong bại liệt $a,b,c$ là những số mang lại trước $a \ne $$0$ hoặc $b \ne 0$ .
- Nếu những số thực ${x_0},\,{y_0}$ vừa lòng $ax + by = c$ thì cặp số $({x_0},\,{y_0})$ được gọi là nghiệm của phương trình $ax + by = c$.
- Trong mặt mũi phẳng lì tọa phỏng $Oxy$ , từng nghiệm $({x_0},\,{y_0})$ của phương trình $ax + by = c$ được màn biểu diễn bươi điểm với tọa phỏng $({x_0},\,{y_0})$.
Tập nghiệm của phương trình số 1 nhị ẩn
Phương trình số 1 nhị ẩn $ax + by = c$ luôn với vô số nghiệm.
Tập nghiệm của phương trình được màn biểu diễn vì như thế đàng thẳng $d:ax + by = c.$
+) Nếu $a \ne 0$ và $b = 0$ thì phương trình với nghiệm $\left\{ \begin{array}{l}x = \dfrac{c}{a}\\y \in R\end{array} \right.$
và đường thẳng liền mạch $d$ song tuy vậy hoặc trùng với trục tung.
+) Nếu $a = 0$ và $b \ne 0$ thì phương trình với nghiệm $\left\{ \begin{array}{l}x \in R\\y = \dfrac{c}{b}\end{array} \right.$
và đường thẳng liền mạch $d$ song tuy vậy hoặc trùng với trục hoành.
+) Nếu $a \ne 0$ và $b \ne 0$ thì phương trình với nghiệm $\left\{ \begin{array}{l}x \in R\\y = - \dfrac{a}{b}x + \dfrac{c}{b}\end{array} \right.$
và đường thẳng liền mạch $d$ là đồ gia dụng thị hàm số $y = - \dfrac{a}{b}x + \dfrac{c}{b}$
2. Các dạng toán thông thường gặp
Dạng 1: Tìm ĐK của thông số nhằm một cặp số mang lại trước là nghiệm của phương trình số 1 nhị ẩn.
Phương pháp:
Nếu cặp số thực $({x_0},\,{y_0})$thỏa mãn $ax + by = c$ thì nó được gọi là nghiệm của phương trình $ax + by = c$.
Dạng 2: Viết công thức nghiệm tổng quát tháo của phương trình số 1 nhị ẩn. Biểu thao diễn tập luyện nghiệm bên trên hệ trục tọa phỏng.
Phương pháp:
Xét phương trình số 1 nhị ẩn $ax + by = c$.
1. Để ghi chép công thức nghiệm tổng quát tháo của phương trình, trước tiên tao màn biểu diễn $x$ theo dõi $y$ ( hoặc $y$ theo dõi $x$) rồi thể hiện công thức nghiệm tổng quát tháo.
2. Để màn biểu diễn tập luyện nghiệm của phương trình bên trên mặt mũi phẳng lì tọa phỏng, tao vẽ đường thẳng liền mạch d với phương trình $ax + by = c$.
Dạng 3: Tìm ĐK của thông số nhằm đường thẳng liền mạch $ax + by = c$ vừa lòng ĐK mang lại trước
Xem thêm: lời bài hát em gái mưa
Phương pháp:
Ta hoàn toàn có thể dùng một số trong những Note tại đây Khi giải dạng toán này:
1. Nếu \(a \ne 0\) và \(b = 0\) thì phương trình đường thẳng liền mạch $d: ax + by = c$ có dạng $d:x = \dfrac{c}{a}$. Khi bại liệt $d$ tuy vậy song hoặc trùng với $Oy$ .
2. Nếu \(a = 0\) và \(b \ne 0\) thì phương trình đường thẳng liền mạch $d: ax + by = c$ với dạng $d:y = \dfrac{c}{b}$. Khi bại liệt $d$ tuy vậy song hoặc trùng với $Ox$ .
3. Đường trực tiếp $d:ax + by = c$ trải qua điểm $M({x_0},\,{y_0})$ Khi và chỉ Khi $a{x_0} + b{y_0} = c$.
Dạng 4: Tìm những nghiệm vẹn toàn của phương trình số 1 nhị ẩn
Phương pháp:
Để mò mẫm những nghiệm vẹn toàn của phương trình số 1 nhị ẩn $ax + by = c$, tao thực hiện như sau:
Cách 1:
Bước 1: Rút gọn gàng phương trình, xem xét cho tới tính phân chia không còn của những ẩn
Bước 2: Biểu thị ẩn nhưng mà thông số của chính nó có mức giá trị vô cùng nhỏ (chẳng hạn $x$ ) theo dõi ẩn bại liệt.
Bước 3: Tách riêng rẽ độ quý hiếm vẹn toàn ở biểu thức của $x$
Bước 4: Đặt ĐK nhằm phân bổ nhập biểu thức của $x$ vì như thế một số trong những nguyên \(t\), tao được một phương trình số 1 nhị ẩn $y$ và \(t\)
- Cứ kế tiếp như bên trên cho tới Khi những ần đều được biểu thị bên dưới dạng một nhiều thức với những thông số vẹn toàn.
Cách 2:
Bước 1. Tìm một nghiệm vẹn toàn $({x_0},\,{y_0})$ của phương trình.
Bước 2. Đưa phương trình về dạng $a(x - {x_0}) + b(y - {y_0}) = 0$ kể từ bại liệt đơn giản và dễ dàng tìm ra những nghiệm vẹn toàn của phương trình tiếp tục mang lại.

![]() Chia sẻ
Chia sẻ
-
Trả tiếng thắc mắc 1 Bài 1 trang 5 Toán 9 Tập 2
a) Kiểm tra coi những cặp số (1; 1) và (0,5; 0)
-
Trả tiếng thắc mắc 2 Bài 1 trang 5 SGK toán 9 tập luyện 2
Trả tiếng thắc mắc 2 Bài 1 trang 5 SGK toán 9 tập luyện 2. Nêu đánh giá về số nghiệm của phương trình 2x – nó = 1.
-
Trả tiếng thắc mắc 3 Bài 1 trang 5 SGK toán 9 tập luyện 2
Trả tiếng thắc mắc 3 Bài 1 trang 5 SGK toán 9 tập luyện 2. Điền nhập bảng sau và ghi chép rời khỏi sáu nghiệm của phương trình (2):...
-
Bài 1 trang 7 SGK Toán 9 tập luyện 2
Trong những cặp số (-2; 1), (0;2), (-1; 0), (1,5; 3) và (4; -3), cặp số này là nghiệm của phương trình:
-
Bài 2 trang 7 SGK Toán 9 tập luyện 2
Với từng phương trình sau, mò mẫm nghiệm tổng quát tháo của phương trình và vẽ đường thẳng liền mạch màn biểu diễn tập luyện nghiệm của nó:
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Xem thêm: công thức tính tỉ lệ gia tăng tự nhiên
Tham Gia Group 2K9 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến lớp 9 và luyện nhập lớp 10 bên trên Tuyensinh247.com, khẳng định hùn học viên lớp 9 học tập đảm bảo chất lượng, trả trả ngân sách học phí nếu như học tập ko hiệu suất cao.










Bình luận