Tam giác nội tiếp đàng tròn xoe - Tất cả những gì bạn phải biết
Chủ đề Tam giác nội tiếp đàng tròn: Tam giác nội tiếp đàng tròn xoe là một trong những định nghĩa cần thiết vô hình học tập. Khi tam giác được nội tiếp đàng tròn xoe, nó dẫn đến một sự phối hợp độc đáo và khác biệt trong những nhân tố hình học tập, tạo nên sự bằng vận và thích mắt. Tam giác nội tiếp đàng tròn xoe cũng đem theo gót những đặc điểm quan trọng đặc biệt, gom tất cả chúng ta hiểu thâm thúy rộng lớn về hình học tập và vận dụng trong số việc thực tiễn.
Bạn đang xem: tam giác nội tiếp đường tròn
Tam giác nội tiếp đàng tròn xoe là một trong những tam giác tuy nhiên một đàng tròn xoe xúc tiếp đối với cả thân phụ cạnh của tam giác cơ. Đường tròn xoe này là đàng tròn xoe nhỏ nhất rất có thể nằm sát vô tam giác và xúc tiếp với những cạnh của tam giác. Tam giác nội tiếp đàng tròn xoe sở hữu tâm trùng với tâm đàng tròn xoe và nửa đường kính vì thế nửa đường kính đàng tròn xoe. Các cạnh của tam giác nội tiếp đường tròn rời nhau bên trên một điểm tạo ra trở nên một gửi gắm điểm chủ yếu tâm. Tam giác nội tiếp đàng tròn xoe có rất nhiều đặc điểm và điểm lưu ý xứng đáng xem xét vô nghành nghề hình học tập và toán học tập.

Tam giác nội tiếp đàng tròn xoe là gì?
Tam giác nội tiếp đàng tròn xoe là tam giác sở hữu đàng tròn xoe xúc tiếp đối với cả thân phụ cạnh của tam giác cơ. Vấn đề này tức là thân phụ điểm xúc tiếp này là vấn đề công cộng của những đoạn trực tiếp nối những đỉnh của tam giác cho tới tâm của đàng tròn xoe nội tiếp. Điểm công cộng của thân phụ đường thẳng liền mạch này được gọi là Trung tâm đàng tròn xoe nội tiếp tam giác. Tam giác nội tiếp đàng tròn xoe sở hữu đặc điểm quan trọng đặc biệt, vô cơ những góc trong những đoạn trực tiếp nối những điểm xúc tiếp với đỉnh của tam giác là như nhau và vì thế 50% góc bên trên những đỉnh của tam giác.
Tam giác nội tiếp đàng tròn xoe sở hữu những điểm lưu ý gì?
Tam giác nội tiếp đàng tròn xoe sở hữu những điểm lưu ý sau đây:
1. Đường tròn xoe nội tiếp tam giác là một trong những đàng tròn xoe sở hữu tâm ở trong tam giác và xúc tiếp với những cạnh tam giác một cơ hội tương đồng. Tức là đàng tròn xoe này trải qua những đỉnh của tam giác và được liên kết với những đỉnh cơ trải qua những đoạn trực tiếp sở hữu chiều lâu năm là nửa đường kính của đàng tròn xoe.
2. Tam giác nội tiếp đàng tròn xoe sở hữu trực tâm, tức là đàng tròn xoe xúc tiếp đối với cả thân phụ cạnh của tam giác. Đây cũng là vấn đề gửi gắm nhau của những đàng trực quan của tam giác.
3. Tam giác nội tiếp đàng tròn xoe sở hữu đàng trung tuyến của tam giác là 2 lần bán kính của đàng tròn xoe. Vấn đề này tức là đàng trung tuyến của tam giác là đàng liên kết trong những điểm vị trí trung tâm những cạnh của tam giác và trải qua tâm của đàng tròn xoe nội tiếp.
4. Diện tích của tam giác nội tiếp đường tròn rất có thể tính vì thế công thức Heron, tức là S = √(p(p-a)(p-b)(p-c)), vô cơ p là nửa chu vi của tam giác (p = (a+b+c)/2) và a, b, c là chừng lâu năm những cạnh của tam giác.
5. Tam giác nội tiếp đàng tròn xoe sở hữu một vài đặc điểm quan trọng đặc biệt, ví dụ như tỉ số những đàng phân giác vô tam giác và tỉ số những cosin vô tam giác đều vì thế nửa đường kính đàng tròn xoe nội tiếp.
Với những điểm lưu ý bên trên, tam giác nội tiếp đường tròn là một trong những định nghĩa cần thiết vô hình học tập và sở hữu phần mềm trong không ít việc và công thức đo lường và tính toán không giống nhau.

Toán 9 Hình 11: Tứ giác nội tiếp Khái niệm trí tuệ rèn luyện kĩ năng lấy gốc
Khám đập phá toàn cầu bí ẩn của tứ giác nội tiếp qua chuyện Clip này! Quý khách hàng sẽ tiến hành học tập cơ hội minh chứng những đặc điểm thú vị và tò mò những phần mềm thực dẫn của tứ giác nội tiếp vô giải toán. Đừng vứt lỡ!
Toán hình Lớp 9 Chứng minh tứ giác nội tiếp đàng tròn
Tạo nên sự thuyết phục với hội chứng minh! Video này tiếp tục khiến cho bạn làm rõ quá trình quan trọng nhằm minh chứng những đẳng thức, đặc điểm và quy tắc vô toán học tập. Cùng kiến thiết trí tuệ minh chứng và phát triển thành một bậc thầy toán học!
Làm thế nào là nhằm tìm ra tâm và nửa đường kính của đàng tròn xoe nội tiếp tam giác?
Để tìm hiểu tâm và nửa đường kính của đàng tròn xoe nội tiếp tam giác, tớ rất có thể tuân theo quá trình sau:
1. Vẽ tam giác ABC.
2. Vẽ đàng trung tuyến của từng cạnh tam giác ABC và gọi những nút giao nhau của đàng trung tuyến là D, E và F.
3. Vẽ đàng vuông góc kể từ A cho tới EF và gửi gắm bên trên điểm G.
4. Vẽ đường thẳng liền mạch EG trải qua G và xúc tiếp với đàng tròn xoe đàng trung tuyến AC bên trên điểm H.
5. Vẽ đường thẳng liền mạch FG trải qua F và xúc tiếp với đàng tròn xoe đàng trung tuyến AB bên trên điểm I.
6. Đường trực tiếp HI là đàng chéo cánh của tam giác ABC.
7. Gọi M là trung điểm của đoạn trực tiếp BC.
8. Vẽ đàng vuông góc kể từ M cho tới HI và gửi gắm bên trên điểm N.
9. Điểm N là tâm của đàng tròn xoe nội tiếp tam giác ABC.
10. Để tìm hiểu nửa đường kính của đàng tròn xoe nội tiếp, tớ chỉ việc đo đoạn trực tiếp NA hoặc NB kể từ tâm N cho tới một trong các nhị đỉnh tam giác A hoặc B.
Lưu ý: Phương pháp này được gọi là cách thức việc bảng vì thế bàn vẽ. Cách không giống nhằm tìm hiểu tâm và nửa đường kính của đàng tròn xoe nội tiếp tam giác là dùng công thức đo lường và tính toán dựa vào lăm le lý thân thích đàng tròn xoe nội tiếp và tam giác.
Đường tròn xoe nội tiếp tam giác xúc tiếp với những cạnh của tam giác ở điểm nào?
Đường tròn xoe nội tiếp tam giác xúc tiếp với những cạnh của tam giác ở điểm nào? Để vấn đáp thắc mắc này, tớ cần thiết làm rõ khái niệm và đặc điểm của đàng tròn xoe nội tiếp tam giác.
Một đàng tròn xoe được gọi là nội tiếp tam giác ABC nếu như và chỉ nếu như tồn bên trên một điểm O ở trong hoặc bên trên cung lồi ABC sao cho những cạnh AB, BC và CA được xúc tiếp với đàng tròn xoe bên trên những điểm M, N, Phường thứu tự.
Theo lăm le lý cơ phiên bản về tam giác, một tam giác nội tiếp đường tròn thì tổng chừng lâu năm những đoạn trực tiếp kể từ những đỉnh tam giác cho tới điểm xúc tiếp vì thế chừng lâu năm chu vi tam giác.
Vậy, nhằm tìm hiểu điểm xúc tiếp của đàng tròn xoe nội tiếp tam giác với những cạnh tam giác, tớ cần thiết tính chu vi tam giác và dùng những lăm le lý tương quan.
1. Tính chu vi tam giác ABC.
2. Tìm điểm xúc tiếp kể từ đỉnh A: Từ điểm O, vẽ một đường thẳng liền mạch tuy nhiên song với đoạn trực tiếp BC. Giao điểm của đường thẳng liền mạch này với cạnh AB là vấn đề M. Điểm M đó là điểm xúc tiếp của đàng tròn xoe với cạnh AB.
3. Tìm điểm xúc tiếp kể từ đỉnh B và C: Tương tự động như bước 2, vẽ những đường thẳng liền mạch tuy nhiên song với đoạn trực tiếp AC và BA. Giao điểm của đường thẳng liền mạch này với những cạnh ứng là vấn đề N và Phường.
Vậy, đàng tròn xoe nội tiếp tam giác tiếp tục xúc tiếp với những cạnh của tam giác bên trên những điểm M, N và Phường.

_HOOK_
Tam giác nội tiếp đàng tròn xoe sở hữu từng nào ngôi trường hợp?
Tam giác nội tiếp đàng tròn xoe sở hữu nhị ngôi trường hợp:
1. Tam giác vuông nội tiếp đàng tròn: Đây là tình huống tam giác sở hữu một góc vuông và đàng tròn xoe nội tiếp xúc tiếp đối với cả thân phụ cạnh của tam giác. Trong tình huống này, đàng tròn xoe nội tiếp được vẽ tựa vô đàng trung tuyến trải qua đỉnh vuông của tam giác. Tam giác vuông này còn có điểm lưu ý là đàng trung tuyến trải qua đỉnh vuông là 2 lần bán kính của đàng tròn xoe nội tiếp.
2. Tam giác ko vuông nội tiếp đàng tròn: Đây là tình huống tam giác không tồn tại góc vuông và đàng tròn xoe nội tiếp ko xúc tiếp đối với cả thân phụ cạnh của tam giác. Trong tình huống này, đàng tròn xoe nội tiếp được vẽ tựa vô trị tuyến của tam giác, tức là đàng tầm từ 1 đỉnh của tam giác cho tới trung điểm của cạnh đối lập với đỉnh cơ.
Tổng thích hợp lại, tam giác nội tiếp đường tròn sở hữu nhị ngôi trường hợp: tam giác vuông và tam giác ko vuông.
Có từng nào tam giác nội tiếp đường tròn vuông?
Để giải việc này, tớ cần thiết xác lập con số tam giác nội tiếp đường tròn vuông.
Đầu tiên, tớ cần phải biết rằng đàng tròn xoe nội tiếp tam giác là đàng tròn xoe nhỏ nhất ở trong tam giác và xúc tiếp đối với cả thân phụ cạnh của tam giác.
Dựa vô đặc điểm này, nhằm xác lập số tam giác nội tiếp đường tròn vuông, tớ đánh giá con số tam giác vuông sở hữu thỏa mãn nhu cầu đặc điểm bên trên.
Một tam giác vuông được xác lập Lúc nhị cạnh của tam giác nằm trong là đàng chéo cánh của một hình vuông vắn, và cạnh loại thân phụ là cạnh của hình vuông vắn. Do cơ, nhằm tìm hiểu con số tam giác nội tiếp đường tròn vuông, tớ cần thiết xác lập con số hình vuông vắn sở hữu cạnh là cạnh của tam giác.
Khi kiểm tra tam giác vuông nội tiếp đàng tròn xoe, cạnh của tam giác là đàng chéo cánh của hình vuông vắn cần là 2 lần bán kính của đàng tròn xoe. Vấn đề này đồng nghĩa tương quan với việc tam giác vuông nội tiếp đàng tròn xoe sở hữu thân phụ cạnh đều nhau.
Vậy nhằm xác lập con số tam giác nội tiếp đường tròn vuông, tớ cần xác lập con số hình vuông vắn sở hữu thân phụ cạnh đều nhau.
Dựa vô những quy tắc về tam giác vuông và hình vuông vắn, tớ hiểu được nếu như một tam giác sở hữu thân phụ cạnh đều nhau, thì tam giác này là tam giác đều. Hơn nữa, nếu như một hình vuông vắn sở hữu hình chữ nhật phía bên trong, thì cạnh của hình vuông vắn đó là cạnh của hình chữ nhật.
Do cơ, nhằm tìm hiểu con số tam giác nội tiếp đường tròn vuông, tớ chỉ việc xác lập con số tam giác đều vô tam giác.
Vậy nhằm xác lập con số tam giác nội tiếp đường tròn vuông, tớ cần thiết xác lập con số tam giác đều vô tam giác.
Tuy nhiên, để hiểu khoảng tầm độ quý hiếm ví dụ của con số tam giác đều, tớ cần thiết tăng vấn đề cụ thể về tam giác ví dụ tuy nhiên chúng ta đang được kiểm tra.
Vì vậy, nhằm vấn đáp thắc mắc này một cơ hội đúng đắn, cần thiết thể hiện vấn đề tăng về tam giác ví dụ và những nhân tố không giống nhằm xác lập con số tam giác nội tiếp đường tròn vuông.
Tam giác khuyếch đại là loại tam giác nào là vô tam giác nội tiếp đường tròn?
Trong tam giác nội tiếp đường tròn, tam giác khuyếch đại là tam giác sở hữu một góc nhọn nằm tại vị trí tâm đàng tròn xoe phía bên trong tam giác. Vấn đề này tức là một góc của tam giác khuyếch đại được bắt gặp kể từ tam giác nước ngoài tiếp đàng tròn xoe to hơn 180 chừng. Tam giác khuyếch đại thông thường sở hữu điểm lưu ý hình học tập quan trọng đặc biệt và rất có thể được dùng nhằm giải quyết và xử lý những việc tương quan cho tới tam giác nội tiếp đường tròn.
Xem thêm: tính từ trong tiếng anh là gì
30s hiểu đàng tròn xoe nội tiếp và đàng tròn xoe nước ngoài tiếp
Đường tròn xoe nội tiếp - kín đáo của những hình học tập thần kỳ! Trong Clip này, các bạn sẽ được tò mò những cách thức vẽ và đo lường và tính toán những đàng tròn xoe nội tiếp với những hình học tập phức tạp. Đừng bỏ qua thời cơ tò mò toàn cầu tuyệt hảo này!
CÁCH VẼ ĐƯỜNG TRÒN NỘI TIẾP TAM GIÁC ĐƠN GIẢN DỄ HIỂU TOÁN LỚP 9
Hãy thuần thục vẽ đàng tròn xoe với Clip này! Quý khách hàng tiếp tục học tập được phương pháp vẽ đàng tròn xoe địa thế căn cứ bên trên những ĐK và đặc điểm đang được học tập từ xưa đến giờ. Mở rộng lớn năng lực vẽ của người sử dụng và dẫn đến những hình vẽ tuyệt đẹp nhất với Clip này.
Điều gì xẩy ra Lúc điểm tâm tư của đàng tròn xoe nội tiếp tam giác trùng với tâm đàng tròn xoe nước ngoài tiếp tam giác?
Khi điểm tâm tư của đàng tròn xoe nội tiếp tam giác trùng với tâm đàng tròn xoe nước ngoài tiếp tam giác, điểm tâm tư và tâm đàng tròn xoe nước ngoài tiếp tiếp tục trùng nhau. Vấn đề này tức là đàng tròn xoe nội tiếp và đàng tròn xoe nước ngoài tiếp nằm trong sở hữu tâm công cộng là một trong những điểm độc nhất.
Để minh chứng điều này, tất cả chúng ta cần thiết làm rõ về khái niệm của những định nghĩa bên trên.
- Đường tròn xoe nội tiếp của tam giác là một trong những đàng tròn xoe nhỏ nhất ở trong tam giác và xúc tiếp đối với cả thân phụ cạnh của tam giác.
- Đường tròn xoe nước ngoài tiếp của tam giác là một trong những đàng tròn xoe lớn số 1 ở ngoài tam giác và xúc tiếp đối với cả thân phụ đỉnh của tam giác.
Với fake thiết là vấn đề tâm tư của đàng tròn xoe nội tiếp tam giác trùng với tâm đàng tròn xoe nước ngoài tiếp tam giác, tớ rất có thể fake sử rằng chừng lâu năm đỉnh cho tới đàng tròn xoe nước ngoài tiếp là đều nhau, tức là đàng tròn xoe nước ngoài tiếp là một trong những đàng tròn xoe đồng tâm với đàng tròn xoe nội tiếp.
Nếu đàng tròn xoe nước ngoài tiếp và đàng tròn xoe nội tiếp nằm trong sở hữu tâm công cộng là một trong những điểm độc nhất, điểm tâm tư và tâm đàng tròn xoe nước ngoài tiếp trùng nhau, thì tức là tam giác này là tam giác đều. Theo khái niệm, tam giác đều là tam giác sở hữu cả thân phụ cạnh và cả thân phụ góc đều nhau.
Vậy, Lúc điểm tâm tư của đàng tròn xoe nội tiếp tam giác trùng với tâm đàng tròn xoe nước ngoài tiếp tam giác, tớ rất có thể tóm lại rằng tam giác này là tam giác đều.
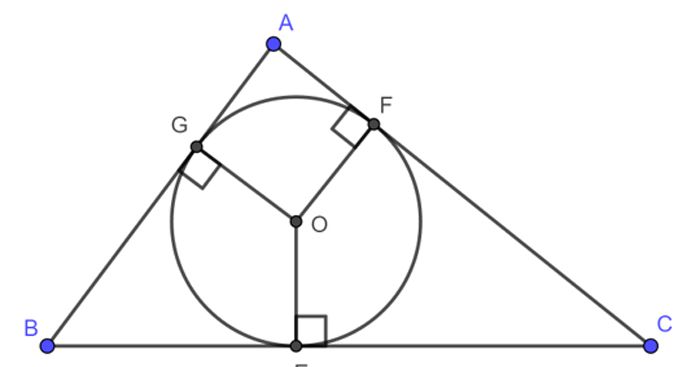
Tam giác nội tiếp đàng tròn xoe sở hữu từng nào chừng lâu năm cạnh vì thế nhau?
Tam giác nội tiếp đàng tròn xoe sở hữu thân phụ chừng lâu năm cạnh đều nhau. Vấn đề này khởi nguồn từ đặc điểm của đàng tròn xoe nội tiếp tam giác. Theo khái niệm, tam giác nội tiếp đường tròn là tam giác tuy nhiên đàng tròn xoe xúc tiếp đối với cả thân phụ cạnh của tam giác. Vì vậy, chừng lâu năm của cạnh nối những đỉnh của tam giác cho tới tâm đàng tròn xoe là đều nhau.
_HOOK_
Tam giác nội tiếp đàng tròn xoe sở hữu từng nào đàng trung trực?
Tam giác nội tiếp đàng tròn xoe sở hữu thân phụ đàng trung trực. Để hiểu điều này, tớ cần phải biết rằng đàng trung trực của một tam giác là đường thẳng liền mạch trải qua trung điểm của một cạnh và vuông góc với cạnh cơ.
Trong tình huống tam giác nội tiếp đường tròn, tớ sở hữu đàng tròn xoe nội tiếp xúc tiếp đối với cả thân phụ cạnh của tam giác. Vì vậy, kể từ trung điểm của từng cạnh tam giác, tớ rất có thể vẽ một đường thẳng liền mạch vuông góc với cạnh cơ và trải qua trung điểm cơ.
Vì tam giác sở hữu thân phụ cạnh, nên tớ cũng có thể có thân phụ trung điểm và vì thế sở hữu thân phụ đàng trung trực ứng. Vấn đề này cũng phù phù hợp với một trong số đặc điểm của tam giác nội tiếp đường tròn là đàng truc trực gửi gắm và trải qua trung điểm.
Vì vậy, tam giác nội tiếp đường tròn sở hữu thân phụ đàng trung trực.
Tam giác nội tiếp đàng tròn xoe sở hữu tồn bên trên vào cụ thể từng tam giác không?
Có, tam giác nội tiếp đường tròn sở hữu tồn bên trên vào cụ thể từng tam giác.
Để minh chứng điều này, tớ kiểm tra những đàng tròn xoe nội tiếp của một tam giác. Đặt tam giác ABC với đàng tròn xoe nội tiếp tâm O.
Ta hiểu được đàng tròn xoe nội tiếp của một tam giác xúc tiếp đối với cả thân phụ cạnh của tam giác. Vì vậy, những điểm xúc tiếp của đàng tròn xoe nội tiếp với những cạnh của tam giác là A, B và C.
Do cơ, tớ sở hữu OA = OB = OC = r, với r là nửa đường kính của đàng tròn xoe nội tiếp. Vấn đề này được minh chứng vì thế đặc điểm của những đàng tròn xoe nội tiếp tam giác.
Vì đàng tròn xoe nội tiếp tam giác luôn luôn tồn bên trên và sở hữu nửa đường kính > 0, nên tớ rất có thể tóm lại rằng tam giác nội tiếp đường tròn tồn bên trên vào cụ thể từng tam giác.
Đường tròn xoe nội tiếp tam giác rất có thể ở ngoài tam giác không?
Đường tròn xoe nội tiếp tam giác ko thể ở ngoài tam giác. Vấn đề này được xác lập vì thế khái niệm của đàng tròn xoe nội tiếp tam giác, là đàng tròn xoe nhỏ nhất xúc tiếp đối với cả thân phụ cạnh của tam giác.
Một đàng tròn xoe nội tiếp tam giác cần xúc tiếp đối với cả thân phụ cạnh của tam giác, chính vì thế nó cần nằm sát vô tam giác. Nếu đàng tròn xoe nội tiếp tam giác ở ngoài tam giác, tức thị nó ko thể xúc tiếp đối với cả thân phụ cạnh, và vì thế ko vừa lòng khái niệm của đàng tròn xoe nội tiếp tam giác.
Vì vậy, đàng tròn xoe nội tiếp tam giác chỉ rất có thể nằm sát vô tam giác và ko thể ở ngoài tam giác.
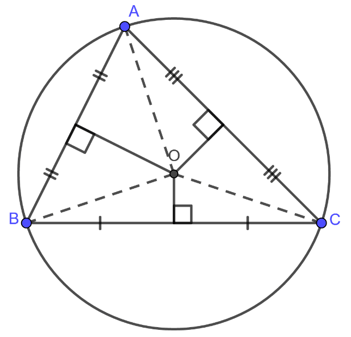
Đường tròn xoe nước ngoài tiếp Đường tròn xoe nội tiếp Bài 8 Toán học tập 9 Cô Vương Thị Hạnh DỄ HIỂU NHẤT
Đường tròn xoe nước ngoài tiếp - nút giao quẹt của việc tinh xảo và thực tiễn! Video này tiếp tục khiến cho bạn làm rõ về đàng tròn xoe nước ngoài tiếp và tìm hiểu hiểu cơ hội xác lập và dùng bọn chúng trong số việc hình học tập phức tạp. Đừng bỏ qua thời cơ phát triển thành một chuyên nghiệp gia!
Làm thế nào là nhằm vẽ được đàng tròn xoe nội tiếp tam giác vì thế khí cụ hình học?
Để vẽ được đàng tròn xoe nội tiếp của một tam giác vì thế khí cụ hình học tập, chúng ta có thể tuân theo quá trình sau:
Bước 1: Vẽ tam giác ABC lên giấy má. Đảm bảo chúng ta đang được biết đầy đủ vấn đề về những cạnh và góc của tam giác này.
Bước 2: Xác lăm le và vẽ đàng trung trực cho từng cạnh của tam giác. Để thực hiện điều này, điểm trung điểm của từng cạnh được xác lập bằng phương pháp nối những đỉnh của tam giác. Khi tớ sở hữu những đàng trung trực cho từng cạnh, tớ sẽ sở hữu thân phụ đoạn trực tiếp trải qua những đỉnh tạo ra trở nên đỉnh của tam giác.
Bước 3: Tìm gửi gắm điểm của thân phụ đàng trung trực đang được vẽ. Điểm gửi gắm nhau này được xem là tâm của đàng tròn xoe nội tiếp tam giác.
Bước 4: Đo chừng lâu năm kể từ tâm cho tới ngẫu nhiên đỉnh nào là của tam giác. Độ lâu năm này được xem là nửa đường kính của đàng tròn xoe nội tiếp.
Bước 5: Sử dụng cây viết và compa (một khí cụ hình học tập rất có thể kiểm soát và điều chỉnh chừng dài) nhằm vẽ đàng tròn xoe với nửa đường kính đang được xác lập kể từ tâm của đàng tròn xoe nội tiếp. Đảm bảo vẽ đàng tròn xoe khá đầy đủ ở trọn vẹn vô tam giác.
Sau Lúc hoàn thiện quá trình bên trên, các bạn sẽ đạt được một đàng tròn xoe nội tiếp tam giác. Hãy chắc chắn rằng rằng những đàng trung trực của tam giác và đàng tròn xoe nội tiếp được vẽ đúng đắn để sở hữu thành quả đích.
Xem thêm: nghị luận về ước mơ
Tam giác nội tiếp đàng tròn xoe sở hữu phần mềm nào là vô thực tế?
Tam giác nội tiếp đàng tròn xoe có rất nhiều phần mềm vô thực tiễn. Dưới đó là một vài ví dụ:
1. Trong technology xây dựng: Tam giác nội tiếp đàng tròn xoe được dùng nhằm tìm hiểu địa điểm kha khá của những nhân tố trong số hình học tập kiến thiết. Ví dụ, một hình chữ nhật rất có thể được xác lập bằng phương pháp xác lập những đàng tròn xoe nội tiếp với từng góc của chính nó. Vấn đề này gom xác lập độ cao thấp, hình dạng và địa điểm của những nhân tố kiến thiết.
2. Trong kiến thiết loại họa: Tam giác nội tiếp đàng tròn xoe là một trong những cấu hình hình học tập cần thiết trong những công việc dẫn đến những hình dạng đẹp nhất và bằng vận trong số hình ảnh, hình đồ họa hoặc kiến thiết hình đồ họa. Việc dùng tam giác nội tiếp đường tròn vô kiến thiết gom dẫn đến những cấu hình hình đồ họa hài hòa và hợp lý và nhất quán.
3. Trong ngành sản xuất: Tam giác nội tiếp đàng tròn xoe được dùng vô tiến độ phát triển nhằm xác xác định trí và khoảng cách trong những nhân tố. Ví dụ, vô quy trình gia công của một cụ thể máy, việc dùng tam giác nội tiếp đường tròn gom xác xác định trí đích của những lỗ, những đàng viền và những nhân tố không giống bên trên mặt phẳng cụ thể.
4. Trong khoa học tập thể thao: Tam giác nội tiếp đàng tròn xoe được dùng nhằm xác lập những chuyên môn và hoạt động trong số môn thể thao như soccer, bóng rổ, những môn bóng quần, etc. Ví dụ, vô soccer, cầu thủ cần được biết phương pháp dùng tam giác nội tiếp đường tròn nhằm xác xác định trí và dịch chuyển mưu trí bên trên Sảnh, kể từ cơ dẫn đến những đàng chuyền và kết hợp hiệu suất cao.
Tổng kết lại, tam giác nội tiếp đường tròn sở hữu phần mềm đặc biệt đa dạng mẫu mã trong số nghành nghề không giống nhau như kiến thiết, kiến thiết hình đồ họa, phát triển và thể thao. Việc hiểu và vận dụng hiệu suất cao tam giác nội tiếp đường tròn rất có thể gom tối ưu hóa việc làm và đạt được thành quả chất lượng tốt rộng lớn trong số nghành nghề này.
_HOOK_
LẤY GỐC HÌNH 9 - CHỨNG MINH TỨ GIÁC NỘI TIẾP ĐƯỜNG TRÒN - PHẦN 1 - THẦY KENKA
\"Bạn mong muốn phát triển thành Chuyên Viên về tam giác nội tiếp đường tròn? Hãy nằm trong Shop chúng tôi tìm hiểu hiểu từng điều chúng ta cần phải biết về chủ thể này trải qua một Clip quan trọng đặc biệt. Nhanh tay nhấn play nhằm chính thức hành trình dài ngục thất phá!\"







Bình luận