tỉ số diện tích của hai tam giác đồng dạng

Cách minh chứng tam giác đồng dạng loại thân phụ vô toán học tập hoàn toàn có thể tiến hành bám theo quá trình sau:
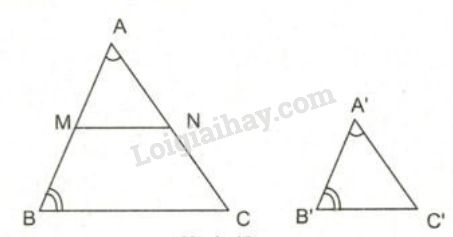
Bước 1: Cho nhì tam giác ABC và A\'B\'C\' sở hữu thân phụ cặp góc ứng cân nhau, tức là ∠A = ∠A\', ∠B = ∠B\', ∠C = ∠C\'.
Bước 2: Kiểm tra tỉ lệ thành phần đồng dạng đằm thắm nhì tam giác. Để thực hiện điều này, tao hoàn toàn có thể đối chiếu phỏng nhiều năm những cạnh ứng của nhì tam giác. Nếu những cạnh ứng sở hữu tỉ lệ thành phần cân nhau, tức là AB/A\'B\' = BC/B\'C\' = AC/A\'C\', thì tao hoàn toàn có thể Kết luận nhì tam giác đồng dạng loại thân phụ.
Bước 3: Nếu ko thể minh chứng được những tỉ lệ thành phần đồng dạng bằng phương pháp đối chiếu phỏng nhiều năm những cạnh, tao hoàn toàn có thể minh chứng đồng dạng bằng phương pháp đối chiếu tỉ số những diện tích S. Để thực hiện điều này, tao tính diện tích S của những tam giác và đối chiếu tỉ số diện tích S. Nếu tỉ số diện tích S của nhì tam giác cân nhau, tức là S(ABC)/S(A\'B\'C\') = AB^2/A\'B\'^2 = BC^2/B\'C\'^2 = AC^2/A\'C\'^2, thì tao hoàn toàn có thể Kết luận nhì tam giác đồng dạng loại thân phụ.
Lưu ý rằng minh chứng đồng dạng loại thân phụ cũng hoàn toàn có thể được tiến hành vì chưng những cách thức không giống nhau, ví như dùng những toan lí và quy tắc rõ ràng. Tuy nhiên, bên trên đấy là một cách thức cơ phiên bản và tổng quan tiền nhằm minh chứng tam giác đồng dạng loại thân phụ vô toán học tập.

Bạn đang xem: tỉ số diện tích của hai tam giác đồng dạng

Tam giác đồng dạng loại thân phụ là nhì tam giác sở hữu những góc ứng cân nhau và tỉ lệ thành phần những cạnh ứng cũng cân nhau. Như vậy tức là nếu như tao kẻ những lối cao của nhì tam giác này, những lối cao tiếp tục tách nhau tạo nên trở nên những tia phân giác tuy vậy tuy vậy. Từ cơ suy rời khỏi tao hoàn toàn có thể xác lập được những tỉ số trong số những cạnh ứng của nhì tam giác.

Để tính tỉ số tam giác đồng dạng loại thân phụ, tất cả chúng ta cần phải biết những điểm lưu ý của nhì tam giác đồng dạng và kể từ cơ vận dụng công thức tính tỉ số.
Công thức tính tỉ số tam giác đồng dạng loại thân phụ là:
tỉ số chu vi tam giác A\'B\'C\' / tỉ số chu vi tam giác ABC = tỉ số phỏng nhiều năm những cạnh tam giác A\'B\'C\' / tỉ số phỏng nhiều năm những cạnh tam giác ABC.
Trong công thức này, \"tỉ số chu vi\" là tỉ số đằm thắm chu vi của nhì tam giác, và \"tỉ số phỏng nhiều năm những cạnh\" là tỉ số đằm thắm phỏng nhiều năm những cạnh ứng của nhì tam giác.
Ví dụ: Nếu tam giác A\'B\'C\' sở hữu chu vi là 4cm và tam giác ABC sở hữu chu vi là 2cm, và những cạnh ứng của nhì tam giác sở hữu tỉ số 1:2, thì tao hoàn toàn có thể tính tỉ số tam giác đồng dạng loại thân phụ bám theo công thức:
4cm / 2cm = tỉ số phỏng nhiều năm những cạnh tam giác A\'B\'C\' / tỉ số phỏng nhiều năm những cạnh tam giác ABC
2 = tỉ số phỏng nhiều năm những cạnh tam giác A\'B\'C\' / 1:2
Bằng cơ hội giải phương trình, tao hoàn toàn có thể tìm ra tỉ số phỏng nhiều năm những cạnh tam giác A\'B\'C\', vô tình huống này tỉ số là 4:1.
Vậy, công thức tính tỉ số tam giác đồng dạng loại thân phụ là tỉ số chu vi tam giác A\'B\'C\' phân tách mang lại tỉ số chu vi tam giác ABC, vì chưng tỉ số phỏng nhiều năm những cạnh ứng của nhì tam giác.

Để minh chứng rằng nhì tam giác đồng dạng loại thân phụ, tao cần thiết xác lập được những điểm lưu ý sau:
1. Xác toan được thân phụ cặp góc ứng vì chưng nhau: Hai tam giác chỉ đồng dạng loại thân phụ Lúc sở hữu những cặp góc ứng cân nhau. Chúng tao cần thiết đối chiếu những góc của nhì tam giác nhằm xác lập coi sở hữu cân nhau hay là không. Nếu những cặp góc ứng vô nhì tam giác đều cân nhau, tao hoàn toàn có thể Kết luận rằng nhì tam giác đồng dạng loại thân phụ.
2. Xác toan được tỉ số đồng dạng: Để minh chứng nhì tam giác đồng dạng loại thân phụ, tao cần thiết xác lập được tỉ số đồng dạng đằm thắm bọn chúng. Tỉ số đồng dạng đằm thắm nhì tam giác được xem bằng phương pháp đối chiếu những cạnh ứng của nhì tam giác. Nếu tỉ số đồng dạng đằm thắm nhì tam giác cân nhau, tao hoàn toàn có thể Kết luận rằng nhì tam giác đồng dạng loại thân phụ.
3. Kiểm tra những ĐK phụ: Ngoài nhì ĐK bên trên, tao cần thiết đánh giá những ĐK phụ không giống nhằm đảm nói rằng nhì tam giác đầy đủ ĐK nhằm đồng dạng loại thân phụ. Các ĐK phụ này gồm những: ĐK nhì cạnh và góc nằm trong lòng nhì cạnh ứng của nhì tam giác cân nhau, hoặc ĐK thân phụ cạnh ứng của nhì tam giác tỉ lệ thành phần cùng nhau.
Tóm lại, nhằm minh chứng rằng nhì tam giác đồng dạng loại thân phụ, tao cần thiết xác lập được những cặp góc ứng cân nhau, tỉ số đồng dạng của nhì tam giác, và đánh giá những ĐK phụ nhằm đáp ứng đầy đủ ĐK cho việc đồng dạng loại thân phụ của nhì tam giác.

Tam giác đồng dạng loại thân phụ là nhì tam giác sở hữu những góc ứng cân nhau và tỉ lệ thành phần trong số những cạnh của bọn chúng cũng cân nhau. Như vậy tức là nhì tam giác này còn có nằm trong cấu tạo hình học tập tuy nhiên sở hữu độ cao thấp không giống nhau.
Một số điểm lưu ý xứng đáng xem xét của tam giác đồng dạng loại thân phụ bao gồm:
1. Tỉ lệ trong số những cạnh của nhì tam giác đồng dạng loại thân phụ là như nhau.
2. Tỉ số này được gọi là tỉ số đồng dạng (tỉ số đồng nhất).
3. Tất cả những góc ứng của nhì tam giác đồng dạng loại thân phụ là cân nhau.
4. Tam giác đồng dạng loại thân phụ hoàn toàn có thể sở hữu độ cao thấp không giống nhau, tuy nhiên dáng vẻ và cấu tạo thông số kỹ thuật đằm thắm bọn chúng không bao giờ thay đổi.
5. Các lối phân giác của những góc ứng phân tách tam giác đồng dạng loại thân phụ trở nên những phần nhỏ sở hữu tỉ lệ thành phần y chang tỉ lệ thành phần trong số những cạnh.
Việc hiểu và vận dụng điểm lưu ý của tam giác đồng dạng loại thân phụ rất rất hữu ích trong các việc giải những vấn đề tương quan cho tới tỉ lệ thành phần và hình học tập tam giác.

Tỉ số của tam giác đồng dạng loại thân phụ không bao giờ thay đổi Lúc tam giác chuyển đổi bám theo một tỉ lệ thành phần vì như thế đồng dạng loại thân phụ là 1 đặc điểm cơ phiên bản của những hình học tập. Khi nhì tam giác đồng dạng loại thân phụ, tỉ số trong số những cặp cạnh ứng của bọn chúng luôn luôn giống như nhau.
Khi chuyển đổi một tam giác bám theo một tỉ lệ thành phần, toàn bộ những cạnh, góc và tỉ số trong số những cặp cạnh ứng đều thay cho thay đổi bám theo và một tỉ lệ thành phần. Nhưng vì như thế tỉ số trong số những cặp cạnh ứng là ko thay đổi, nên tỉ số tam giác đồng dạng loại thân phụ cũng không bao giờ thay đổi.
Việc không thay đổi tỉ số tam giác đồng dạng loại thân phụ Lúc tam giác chuyển đổi bám theo một tỉ lệ thành phần rất rất hữu ích trong các việc giải quyết và xử lý những vấn đề hình học tập. Nó được chấp nhận tao vận dụng những nguyên tắc tam giác đồng dạng như cân nặng sựa tam giác và dò la tỉ số chiều nhiều năm những cạnh, góc và diện tích S nhưng mà ko cần phải biết độ quý hiếm đúng đắn của bọn chúng.
Đồng thời, đặc điểm này cũng hỗ trợ chúng ta nắm được quan hệ trong số những hình học tập vô không khí và là 1 trong mỗi hạ tầng cần thiết của toan thức ma mãnh trận.

Để dò la một tam giác đồng dạng loại thân phụ với 1 tam giác vẫn mang lại, tao cần thiết thực hiện quá trình sau:
Bước 1: Xác toan thân phụ đỉnh của tam giác vẫn cho: A, B và C.
Bước 2: Xác toan tỉ số đồng dạng đằm thắm nhì tam giác: Tỉ số này hoàn toàn có thể là tỉ số phỏng nhiều năm những cạnh, tỉ số diện tích S hoặc tỉ số góc trong số những cạnh ứng. Nếu không tồn tại vấn đề cụ thể, tao hoàn toàn có thể fake sử tỉ số đồng dạng là k.
Bước 3: Xây dựng tam giác đồng dạng loại thân phụ với tam giác vẫn mang lại. Ta hoàn toàn có thể thực hiện như sau:
- Chọn một điểm O ngẫu nhiên.
- Từ O, vẽ đường thẳng liền mạch trải qua A và kẻ một quãng trực tiếp con cái OA\' có tính nhiều năm ứng là k đợt đoạn trực tiếp OA.
- Từ A\', vẽ đường thẳng liền mạch trải qua B và kẻ một quãng trực tiếp con cái A\'B\' có tính nhiều năm ứng là k đợt đoạn trực tiếp A\'B.
- Cuối nằm trong, kể từ B\', vẽ đường thẳng liền mạch trải qua C và kẻ một quãng trực tiếp con cái A\'B\'C\' có tính nhiều năm ứng là k đợt đoạn trực tiếp A\'B\'.
Với quá trình bên trên, tao vẫn tìm ra tam giác đồng dạng loại thân phụ với tam giác vẫn mang lại.

Tam giác đồng dạng loại thân phụ không tồn tại tương quan thẳng cho tới việc tính số liệu vô địa hình hoặc design hình đồ họa. Tam giác đồng dạng loại thân phụ là định nghĩa vô toán học tập, nó chỉ nhắc đến quan hệ trong số những tam giác sở hữu những góc tương đương nhau và tỉ lệ thành phần những cạnh tương tự động nhau. Tuy nhiên, vô nghành nghề dịch vụ design hình đồ họa, nguyên tắc đồng dạng được vận dụng phổ cập để thay thế thay đổi độ cao thấp và dáng vẻ của những hình vẽ, bao hàm cả tam giác.

Tam giác đồng dạng loại thân phụ cũng đều có phần mềm trong tương đối nhiều nghành nghề dịch vụ không giống ngoài toán học tập. Một số nghành nghề dịch vụ và phần mềm rõ ràng của tam giác đồng dạng loại thân phụ bao gồm:
1. Địa lý: Trong địa lý, nguyên tắc tam giác đồng dạng được vận dụng nhằm đo lường và tính toán những tỷ trọng và khoảng cách. Ví dụ, trong những khi kiến tạo phiên bản trang bị hoặc phiên bản trang bị địa hình, tam giác đồng dạng loại thân phụ được dùng nhằm đo lường và ánh xạ những đối tượng người dùng bên trên mặt mũi khu đất lên phiên bản trang bị.
2. Kiến trúc: Tam giác đồng dạng loại thân phụ cũng khá được dùng vô design phong cách thiết kế sẽ tạo rời khỏi những kết cấu sở hữu tỉ lệ thành phần đẹp nhất và hợp lý. Các mái ấm design phong cách thiết kế dùng nguyên tắc tam giác đồng dạng sẽ tạo rời khỏi những phiên bản vẽ và quy mô nhằm đánh giá những công trình xây dựng phong cách thiết kế đa dạng và phong phú.
3. Nhiếp ảnh: Trong nhiếp hình ảnh, dùng tam giác đồng dạng loại thân phụ sẽ tạo rời khỏi những tấm hình sở hữu tỉ lệ thành phần và tầm nhìn thích mắt. Việc hiểu và vận dụng nguyên tắc tam giác đồng dạng gom những thợ chụp ảnh bố trí, cân đối và đưa đến những quang cảnh sở hữu tỉ lệ thành phần hợp lí và thẩm mỹ và làm đẹp.
4. Đồ họa máy tính: Trong nghành nghề dịch vụ hình đồ họa PC, nguyên tắc tam giác đồng dạng loại thân phụ được dùng nhằm chuyển đổi và khởi tạo hình hình ảnh. Các ứng dụng hình đồ họa PC dùng những công thức và thuật toán dựa vào nguyên tắc tam giác đồng dạng nhằm thu nhỏ, phóng to lớn hoặc chuyển đổi những đối tượng người dùng, hình hình ảnh bên trên screen.
5. Kỹ thuật và xây dựng: Tam giác đồng dạng loại thân phụ được dùng thoáng rộng trong những công trình xây dựng kiến tạo và chuyên môn nhằm đo lường và tính toán những tỉ lệ thành phần và khoảng cách. Ví dụ, vô nghành nghề dịch vụ đo lường, tam giác đồng dạng được dùng nhằm đo lường khoảng cách và diện tích S của những đối tượng người dùng vô không khí.
Trên đấy là một số trong những nghành nghề dịch vụ và phần mềm của tam giác đồng dạng loại thân phụ ngoài nghành nghề dịch vụ toán học tập. Tam giác đồng dạng loại thân phụ sở hữu những đặc điểm quan trọng đặc biệt nhưng mà hoàn toàn có thể được vận dụng trong tương đối nhiều ngành nghề ngỗng không giống nhau nhằm giải quyết và xử lý những vấn đề thực tiễn.

Trong tam giác đồng dạng loại thân phụ, sở hữu những bộ phận cần thiết chú ý nhằm hiểu và vận dụng định nghĩa này hiệu suất cao như sau:
1. Các cặp góc tương đồng: Trong tam giác đồng dạng loại thân phụ, những góc ứng của nhì tam giác đồng dạng cân nhau. Như vậy tức là nếu như những góc vô một tam giác được đo vì chưng những góc ứng vô tam giác cơ, thì bọn chúng sẽ sở hữu nằm trong độ quý hiếm.
2. Tỉ lệ những cạnh: Tỉ lệ trong số những cạnh của nhì tam giác đồng dạng loại thân phụ cũng cân nhau. Nếu một cạnh của tam giác gốc được nhân với 1 tỉ lệ thành phần chắc chắn, toàn bộ những cạnh của tam giác đồng dạng tiếp tục cũng nên được nhân với tỉ lệ thành phần cơ.
3. Tương tự động, tỉ lệ thành phần trong số những lối điểm vô tam giác đồng dạng cũng nên giống như nhau. Như vậy bao hàm tỉ lệ thành phần trong số những lối phân giác, lối cao, lối trung tuyến và những lối điểm không giống.
4. Tỉ lệ diện tích S: Diện tích của nhì tam giác đồng dạng cũng tỉ lệ thành phần cùng nhau bám theo bình phương tỉ lệ thành phần của những cạnh ứng. Như vậy tức là nếu như tỉ lệ thành phần đằm thắm nhì cạnh ứng là a/b, thì tỉ lệ thành phần diện tích S đằm thắm nhì tam giác là a^2/b^2.
5. Các đặc điểm được vận dụng trong các việc giải bài bác toán: Tam giác đồng dạng loại thân phụ hỗ trợ một số trong những đặc điểm cần thiết, như lối cao của tam giác, tỉ lệ thành phần diện tích S và những đối sánh trong số những dạng tam giác không giống. Như vậy hoàn toàn có thể được dùng nhằm giải những vấn đề về tam giác đồng dạng và vận dụng vô thực tiễn.
Để hiểu và vận dụng hiệu suất cao định nghĩa tam giác đồng dạng loại thân phụ, cần thiết chú ý nắm rõ những trở nên phần bên trên và vận dụng bọn chúng một cơ hội đúng đắn trong các việc giải quyết và xử lý những vấn đề tương quan cho tới tam giác.

Xem thêm: bài tập câu bị đông trong tiếng anh