Tuyển tập đề thi học sinh giỏi môn Toán lớp 6 (có đáp án)

Bộ đề đua học viên chất lượng môn Toán lớp 6

Tuyển tập luyện đề đua học viên chất lượng môn Toán lớp 6 (có đáp án) tổ hợp nhiều đề đua HSG Toán với nội dung bám sát công tác học tập bám theo đòi hỏi và quy ấn định của Sở GD&ĐT. Mời chúng ta vận chuyển về xem thêm cụ thể.

Bạn đang xem: đề thi học sinh giỏi toán 6

Lưu ý: Nếu không kiếm thấy nút Tải về nội dung bài viết này, các bạn sướng lòng kéo xuống cuối nội dung bài viết nhằm vận chuyển về.

ĐỀ THI THAM KHẢO

(Thời gian giảo thực hiện bài bác 120 phút, ko kể thời hạn gửi gắm đề)

ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG LẦN 1

Môn: TOÁN - Lớp 6

Bài 1:(3 điểm)

a) Thực hiện tại quy tắc tính b) Rút gọn gàng biểu thức

b) 2³. 5³- 3 {400 -[ 673 - 2(7⁸ : 7⁶ + 1²⁰²¹)]}

Bài 2: (4,0 điểm)

Tìm số đương nhiên x biết:

a) x + (x + 1) + (x + 2) + …+ (x + 99) = 5450.

b) 3.(5^x- 1) - 2 = 70.

c) 2^x+ 2^{x + 1} + 2^{x + 2} = 960 - 2^{x + 3}

Bài 3: (3 điểm) Chứng tỏ rằng:

a) (3¹⁰⁰+19⁹⁹⁰) 2

b) Tổng của 4 số đương nhiên liên tục ko phân tách không còn mang đến 4

Bài 4 (6,0 điểm)

a) và

b)Tìm số đương nhiên a nhỏ nhất sao cho: a phân tách mang đến 2 dư 1, a phân tách mang đến 3 dư 1, a phân tách mang đến 5 dư 4, a phân tách mang đến 7 dư 3.

c) Cho p là số nhân tố (p > 3) và 2p + 1 cũng chính là số nhân tố. Hỏi 4p + một là số nhân tố hoặc hợp ý số? Vì sao?

Bài 5 (4,0 điểm)

Một nửa số dù vuông của 1 bàn cờ 8x8 được tô đen sạm như hình vẽ sau. Có toàn bộ từng nào hình vuông vắn 2x2, 4x4, 6x6 nhưng mà mang trong mình một nửa số dù vuông được tô đen?

………….. Hết …………

>> Chi tiết đáp án ở nhập FILE TẢI VỀ MIỄN PHÍ <<

Đề đua học viên chất lượng lớp 6 môn Toán số 1

PHÒNG GD&ĐT HUYỆN TƯ NGHĨA

KÌ THI HỌC SINH GIỎI CẤP HUYỆN
Môn thi: Toán 6
Thời gian: 150 phút (không kể thời hạn gửi gắm đề)

Câu 1. (3,0 điểm) Cho $A=\frac{12 n+1}{2 n+3}$ . Tìm độ quý hiếm của n để:

a) A là 1 trong những phân số.

b) A là một trong những nguyên

Câu 2. (4,0 điểm)

a) Không quy đồng hãy tính tổng sau: $A=\frac{-1}{20}+\frac{-1}{30}+\frac{-1}{42}+\frac{-1}{56}+\frac{-1}{72}+\frac{-1}{90}$

b) So sánh Phường và Q, biết: $\mathrm{P}=\frac{2010}{2011}+\frac{2011}{2012}+\frac{2012}{2013}$ và $\mathrm{Q}=\frac{2010+2011+2012}{2011+2012+2013}$

Câu 3. (3,0 điểm): Tìm x, biết:

a) (7x - 11)³ = 2⁵.5² + 200

b) $3\frac{1}{3}$ x + $16\frac{3}{4}$ = - 13,25

Câu 4. (3,0 điểm) Tại lớp 6A, số học viên chất lượng học tập kỳ I vì như thế $\frac{3}{7}$ số sót lại. Cuối năm đạt thêm 4 học viên đạt loại chất lượng nên số học viên chất lượng vì như thế $\frac{2}{3}$ số sót lại. Tính số học viên của lớp 6A.

Câu 5. (2,0 điểm) Cho $\overline{a b a b a b}$ là số đem sáu chữ số, minh chứng $\overline{a b a b a b}$ số là bội của 3.

Câu 6. (5,0 điểm) Cho góc xAy, bên trên tia Ax lấy điểm B sao mang đến AB = 5 centimet. Trên tia đối của tia Ax lấy điểm D sao mang đến AD = 3 centimet, C là 1 trong những điểm bên trên tia Ay.

a) Tính BD.

b) thạo góc BCD = 85^o, góc BCA = 50^o. Tính ACD

c) thạo AK = 1 centimet (K nằm trong BD). Tính BK

Đáp án đề đua học viên chất lượng môn Toán lớp 6 - Số 1

Đáp án đề đua học viên chất lượng môn Toán lớp 6

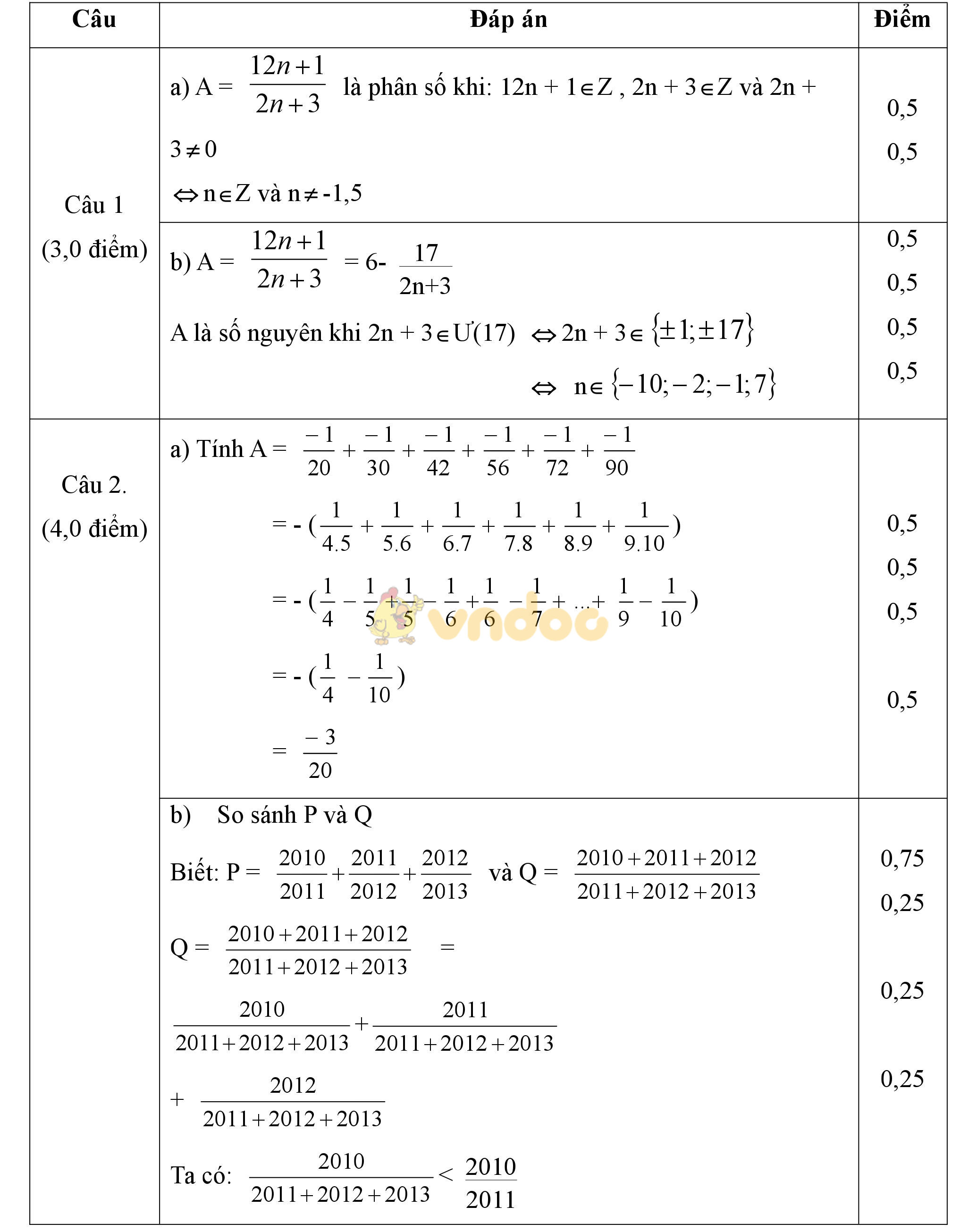
Đề đua học viên chất lượng môn Toán lớp 6 số 2

SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH ĐỒNG THÁP
ĐỀ CHÍNH THỨC
(Đề bao gồm đem 01 trang)

KIỂM TRA KHẢO SÁT HỌC SINH ĐỘI TUYỂN
Môn kiểm tra: TOÁN – LỚP 6
Thời gian: 150 phút (không kể thời hạn phân phát đề)

Câu I: (4.0 điểm). Thực hiện tại quy tắc tính

1) $\mathrm{A}=\frac{5 \cdot\left(2^{2} \cdot 3^{2}\right)^{9} \cdot\left(2^{2}\right)^{6}-2 \cdot\left(2^{2} \cdot 3\right)^{14} \cdot 3^{4}}{5 \cdot 2^{28} \cdot 3^{18}-7 \cdot 2^{29} \cdot 3^{18}}$

2) $\mathrm{B}=81 \cdot\left[\frac{12-\frac{12}{7}-\frac{12}{289}-\frac{12}{85}}{4-\frac{4}{7}-\frac{4}{289}-\frac{4}{85}}: \frac{5+\frac{5}{13}+\frac{5}{169}+\frac{5}{91}}{6+\frac{6}{13}+\frac{6}{169}+\frac{6}{91}}\right] \cdot \frac{158158158}{711711711}$

Câu II: (4.0 điểm)

1) So sánh Phường và Q

Biết $\mathrm{P}=\frac{2010}{2011}+\frac{2011}{2012}+\frac{2012}{2013}$ và $\mathrm{Q}=\frac{2010+2011+2012}{2011+2012+2013}$

2) Tìm nhì số đương nhiên a và b, biết: BCNN(a, b) = 420; ƯCLN(a, b) = 21 và a + 21 = b.

Câu III: (4.0 điểm)

1) Chứng minh rằng: Nếu 7x + 4y ⋮ 37 thì 13x +18y ⋮ 37

2) Cho $\mathrm{A}=\frac{1}{2}+\frac{3}{2}+\left(\frac{3}{2}\right)^{2}+\left(\frac{3}{2}\right)^{3}+\left(\frac{3}{2}\right)^{4}+\ldots+\left(\frac{3}{2}\right)^{2012} \text { và } \mathrm{B}=\left(\frac{3}{2}\right)^{2013}: 2$

Tính B – A

Câu IV. (6.0 điểm)

Cho xÂy, bên trên tia Ax lấy điểm B sao mang đến AB = 6 centimet. Trên tia đối của tia Ax lấy điểm D sao mang đến AD = 4 centimet.

1) Tính BD.

2) Lấy C là 1 trong những điểm bên trên tia Ay. thạo BĈD = 80^o, BĈA = 45^o. Tính AĈD

3) thạo AK = 2 centimet (K nằm trong BD). Tính BK

Câu V: (2.0 điểm)

Xem thêm: đại học hàng hải điểm chuẩn

1) Tìm những số đương nhiên x, y chang cho: $\frac{x}{9}-\frac{3}{y}=\frac{1}{18}$

2) Tìm số đương nhiên n nhằm phân số $B=\frac{10 n-3}{4 n-10}$ đạt GTLN. Tìm độ quý hiếm lớn số 1 đó

Đáp án đề đua học viên chất lượng môn Toán lớp 6 - Số 2

Đáp án đề đua học viên chất lượng môn Toán lớp 6

Đề đua học viên chất lượng lớp 6 môn Toán số 3

Câu 1 (2,0 điểm)

a) Tính nhanh: 16 + (27 - 7.6) - (94.7 - 27. 99)

b) Tính tổng: A = Đề đua HSG Toán lớp 6

Câu 2 (2,0 điểm) Cho biểu thức: M = 5 + 5² + 5³ + … + 5⁸⁰. Chứng tỏ rằng:

a) M phân tách không còn mang đến 6.

b) M ko cần là số chủ yếu phương.

Câu 3 (2,0 điểm)

a) Chứng tỏ rằng: (n ∈ N) là phân số tối giản.

b) Tìm những độ quý hiếm nguyên vẹn của n nhằm phân số B = có độ quý hiếm là số nguyên vẹn.

Câu 4 (1,0 điểm) Tìm số đương nhiên nhỏ nhất sao mang đến Lúc phân tách số cơ mang đến 3 dư 1; phân tách mang đến 4 dư 2; phân tách mang đến 5 dư 3; phân tách mang đến 6 dư 4 và phân tách không còn mang đến 11.

Câu 5 (2,0 điểm) Trên nằm trong nửa mặt mày phẳng phiu bờ chứa chấp tia Ox vẽ 3 tia Oy, Oz, Ot sao cho

a) Tính góc yOz và góc zOt

b) Trong 3 tia Oy, Oz, Ot tia nào là nằm trong lòng 2 tia còn lại? Vì sao?

c) Chứng minh: Oz là tia phân giác của góc yOt.

Câu 6 (1,0 điểm) Chứng minh rằng: 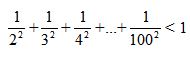Đề đua HSG Toán lớp 6

Đề đua học viên chất lượng lớp 6 môn Toán số 4

Câu 1 (1,5 điểm): Thực hiện tại quy tắc tính.

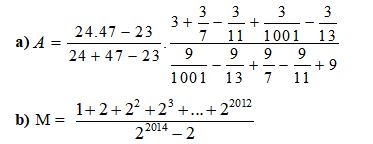
Đề đua HSG Toán lớp 6

Câu 2 (2,5 điểm)

a) Cho S = 5 + 5²+ 5³ + 5⁴ + 5⁵ + 5⁶+…+ 5²⁰¹². Chứng tỏ S phân tách không còn mang đến 65.

b) Tìm số đương nhiên nhỏ nhất sao mang đến Lúc phân tách mang đến 11 dư 6, phân tách mang đến 4 dư 1và phân tách mang đến 19 dư 11.

c) Chứng tỏ: A = 10ⁿ+ 18n - 1 phân tách không còn mang đến 27 (với n là số tự động nhiên)

Câu 3 (2,0 điểm)

a)Tìm x, hắn nguyên vẹn biết : 2x (3y – 2) + (3y – 2) = -55

b) Chứng minh rằng: Đề đua HSG Toán lớp 6

Câu 4 (2,5 điểm): Cho nửa mặt mày phẳng phiu bờ AB chứa chấp nhì tia đối OA và OB.

a) Vẽ tia OC tạo ra với tia OA một góc vì như thế a^o, vẽ tia OD tạo ra với tia OCC một góc vì như thế (a + 10)^ovà với tia OB một góc vì như thế (a + 20)^o. Tính a^o

b) Tính góc xOy, biết góc AOx vì như thế 22^ovà góc BOy vì như thế 48^o

c) Gọi OE là tia đối của tia OD, tính số đo góc kề bù với góc xOD Lúc góc AOC vì như thế a^o

Câu 5 (1,5 điểm): Cho

a) Chứng minh rằng A phân tách không còn mang đến 24

b) Chứng minh rằng A ko cần là số chủ yếu phương.

Đề đua học viên chất lượng lớp 6 môn Toán số 5

Bài 1 (4,5 điểm) Tính độ quý hiếm những biểu thức sau:

a. A = $\frac{2}{3}+\frac{5}{6}: 5-\frac{1}{18} \cdot(-3)^{2}$

b. B = 3.{5.[(5² + 2³): 11] - 16} + 2015

c. $\mathrm{C}=\left(1+\frac{1}{1.3}\right)\left(1+\frac{1}{2.4}\right)\left(1+\frac{1}{3.5}\right) \ldots\left(1+\frac{1}{2014.2016}\right)$

Bài 2 (4,0 điểm)

a. Tìm số tự nhiên x biết 8.6 + 288 : (x - 3)² = 50

b. Tìm những chữ số x; hắn nhằm A = x183y phân tách mang đến 2; 5 và 9 đều dư 1.

c. Chứng tỏ rằng nếu p là số nguyên vẹn tố lớn rộng lớn 3 thì p² - 1 phân tách hết mang đến 3.

Bài 3 (4,5 điểm)

a. Cho biểu thức: $B=\frac{5}{n-3}$ (n ∈ Z, n ≠ 3)

Tìm tất cả các giá trị nguyên vẹn của n để B là số nguyên vẹn.

b. Tìm những số nhân tố x, y chang cho: x² + 117 = y²

c. Số 2¹⁰⁰ viết nhập hệ thập phân có từng nào chữ số .

Bài 4 (5,0 điểm)

Cho góc $\widehat{x B y}=55^{0}$ . Trên những tia Bx; By thứu tự lấy những điểm A; C

(A ≠ B; C ≠ B). Trên đoạn trực tiếp AC lấy điểm D sao mang đến = 30^o

a. Tính chừng nhiều năm AC, biết AD = 4cm, CD = 3cm.

b. Tính số đo của góc DBC.

c. Từ B vẽ tia Bz sao mang đến $\widehat{D B z}=90^{0}$ . Tính số đo của góc ABz.

Bài 5 (2,0 điểm)

a. Tìm những chữ số a, b, c không giống 0 thỏa mãn: $\overline{\mathrm{abbc}}=\overline{\mathrm{ab}} \times \overline{\mathrm{ac}} \times 7$

Xem thêm: f là gì trong vật lý

b. Cho $\mathrm{A}=\frac{1}{2}\left(7^{2012^{2015}}-3^{92^{94}}\right)$ . Chứng minh A là số đương nhiên phân tách không còn mang đến 5

---------------------------------

Để sẵn sàng mang đến kì đua học viên chất lượng tiếp đây, mời mọc chúng ta nhập thể loại Thi học viên chất lượng bên trên VnDoc. Chuyên mục tổ hợp đề đua HSG lớp 6 của toàn bộ những môn, là tư liệu hoặc cho những em học viên ôn tập luyện và cũng chính là tư liệu hoặc mang đến thầy cô ôn luyện group tuyển chọn học viên chất lượng của tớ.