nguyên hàm cos bình x

Để mò mẫm công thức vẹn toàn hàm của hàm số sin bình x, tất cả chúng ta hoàn toàn có thể dùng công thức hạ bậc hoặc những công thức lượng giác cơ bạn dạng.
Công thức hạ bậc:
∫sin^2xdx = ∫(1 - cos^2x)dx
Ta tiếp tục tiến hành tích phân của từng bộ phận nhập công thức trên:
∫(1 - cos^2x)dx = ∫(1 - cosx)(1 + cosx)dx
Áp dụng quy tắc nhân khai quật đối tác chiến lược, tớ có:
∫(1 - cos^2x)dx = ∫(1 - cos^2x)dx + ∫(cosx - cos^3x)dx
Tiếp theo gót, tất cả chúng ta tính từng phần riêng biệt biệt:
∫dx = x + C1
∫cosx dx = sinx + C2
∫cos^3x dx = ∫cosx(1 - sin^2x)dx = ∫cosx - sin^2xcosx dx
= sinx - ∫sin^2xdx
= sinx - ∫(1 - cos^2x)dx
= sinx - x + ∫cos^2xdx
= sinx - x + ∫(1 - sin^2x)dx
= sinx - x + x - ∫sin^2xdx
= sinx - x + x - ∫(1 - cos^2x)dx
= sinx - x + x - (x - ∫cos^2xdx)
Kết hợp ý những bộ phận, tớ có:
∫sin^2xdx = x + C1 + sinx + C2 - x + x - (x - ∫cos^2xdx)
= sinx + x + C
Do cơ, công thức vẹn toàn hàm của hàm số sin bình x là ∫sin^2xdx = sinx + x + C.
Lưu ý: Trong quy trình đo lường và tính toán, tất cả chúng ta vận dụng những phép tắc thay đổi và quy tắc tích phân trải qua kỹ năng đang được biết về tích phân và công thức hạ bậc.

Bạn đang xem: nguyên hàm cos bình x

Công thức được dùng nhằm tính vẹn toàn hàm của hàm số sin bình x là:
∫sin^2(x)dx = ∫(1 - cos(2x))/2 dx
= (1/2)x - (1/4)sin(2x) + C
Với C là hằng số nằm trong.

Để trả hàm số sin bình x về dạng lượng giác cơ bạn dạng nhằm tính vẹn toàn hàm, tớ dùng công thức hạ bậc. Công thức hạ bậc mang lại nồng độ giác cơ bạn dạng là:
sin²x = 1 - cos²x
Áp dụng công thức hạ bậc, tớ có:
∫sin²xdx = ∫(1 - cos²x)dx
Sau cơ, tớ tính vẹn toàn hàm của một và tính vẹn toàn hàm của -cos²x.
Nguyên hàm của một là x và vẹn toàn hàm của -cos²x hoàn toàn có thể được xem bằng phương pháp dùng công thức vẹn toàn hàm của cosin hạng 2:
∫cos²xdx = ∫(1 + cos2x)/2 dx = (x + sin2x)/2 + C
Do cơ, vẹn toàn hàm của hàm số sin bình x được xem bằng phương pháp phối kết hợp sản phẩm kể từ nhì phần trên:
∫sin²xdx = x/2 + sin2x/2 + C
Trong cơ C là hằng số.

Để tính vẹn toàn hàm của hàm số sin nón nhì x, tớ hoàn toàn có thể dùng công thức hạ bậc. Công thức này được cho phép tất cả chúng ta trả về mò mẫm vẹn toàn hàm của hàm con số giác cơ bạn dạng.
Cụ thể, nhằm mò mẫm vẹn toàn hàm của sin nón nhì x, tớ hoàn toàn có thể vận dụng công thức hạ bậc sau:
∫sin^2(x)dx = ∫(1 - cos^2(x))dx
Khi dùng công thức này, tớ tiến hành việc thay cho thế cos^2(x) vì chưng 1 - sin^2(x) nhằm giản dị hóa biểu thức. Sau cơ, tớ tính vẹn toàn hàm của từng bộ phận nhập biểu thức.
Để tính vẹn toàn hàm của một, tớ có:
∫1 dx = x + C1
Để tính vẹn toàn hàm của cos^2(x), tớ hoàn toàn có thể dùng công thức nằm trong sinh:
cos^2(x) = (1 + cos(2x))/2
Đặt u = cos(2x), thì du = -2sin(2x)dx. bằng phẳng cơ hội quy đổi đổi mới và thay cho thế, tớ có:
∫(1 - cos^2(x))dx = ∫(1 - (1 + cos(2x))/2) dx
= ∫(1/2 - 1/2cos(2x)) dx
= 1/2∫dx - 1/2∫cos(2x)dx
= 1/2x - 1/4sin(2x) + C2
Kết hợp ý sản phẩm của tất cả nhì bộ phận, tớ đem sản phẩm sau cuối là:
∫sin^2(x)dx = x/2 - 1/4sin(2x) + C
Với C là hằng số tùy ý.

Để tính vẹn toàn hàm của hàm số sin nhì x, tớ hoàn toàn có thể dùng công thức hạ bậc. Với hàm số f(x) = sin2x, tớ vận dụng công thức hạ bậc để mang về dạng vẹn toàn hàm của hàm con số giác cơ bạn dạng.
Công thức hạ bậc mang lại hàm sin2x là: ∫sin2xdx = ∫(1-cos2x)/2dx.
Cuối nằm trong, tớ tính được vẹn toàn hàm của hàm số sin nhì x là: ∫sin2xdx = ∫(1-cos2x)/2dx.
Vì vậy, nhằm tính được vẹn toàn hàm của hàm số sin nhì x, tớ dùng công thức hạ bậc và tiến hành công việc đo lường và tính toán ứng.

Để tính vẹn toàn hàm của cos^2x, tớ hoàn toàn có thể dùng nhì công thức thân thuộc sau:
1. Công thức hạ bậc: ∫cos^2(x)dx = ∫(1 + cos2x)/2 dx
Bằng cơ hội phân chia tử số trở nên nhì phần, tớ hoàn toàn có thể tính vẹn toàn hàm của từng phần riêng biệt rẽ.
∫(1 + cos2x)/2 dx = ∫(1/2 + cos2x/2) dx = (1/2)x + (sin2x)/4 + C
Với C là hằng số nhập quy trình tính vẹn toàn hàm.
2. Công thức thay đổi lượng giác: ∫cos^2(x)dx = ∫1/2(1 + cos2x) dx
Ước lượng cos2x bằng phương pháp dùng công thức lượng giác cơ bạn dạng cos2x = (1 + cos(2x))/2:
∫1/2(1 + cos2x) dx = ∫1/2(1 + (1 + cos(2x))/2) dx
= ∫1/2(3/2 + cos(2x)/2) dx = (3/4)x + (sin(2x))/4 + C
Vậy tớ hoàn toàn có thể tính vẹn toàn hàm của cos^2x bằng phương pháp dùng công thức hạ bậc hoặc công thức thay đổi lượng giác như bên trên.

Để tính vẹn toàn hàm của hàm số sin nón n x, tớ hoàn toàn có thể dùng công thức hạ bậc để mang về mò mẫm vẹn toàn hàm của hàm con số giác cơ bạn dạng.
Công thức hạ bậc: ∫sin^nx dx = ∫(1 - cos^2 x)^(n/2) dx
Đầu tiên, tớ thay cho thế sin^2 x = 1 - cos^2 x nhập công thức bên trên, tớ được:
∫sin^nx dx = ∫(1 - cos^2 x)^(n/2) dx
Sau cơ, tớ tiến hành phép tắc thay đổi đổi mới số, bịa đặt u = cos x. Khi cơ, du = -sin x dx.
Đổi đổi mới số nhập công thức, tớ có:
∫(1 - cos^2 x)^(n/2) dx = -∫(1 - u^2)^(n/2) du
Tiếp theo gót, tớ tiến hành phân tan trở nên tổng những phân thức hợp lý và phải chăng bằng phương pháp dùng tấp tểnh lý nhân đại số:
(1 - u^2)^(n/2) = (1 - u) * (1 + u) * (1 - u^2)^(n/2 - 1)
Quá trình phân tan tiếp tục nối tiếp cho tới Khi chỉ từ lại những phân thức đem dạng (1 - u).
Sau cơ, tớ tính vẹn toàn hàm của từng phân thức bằng phương pháp dùng quy tắc tính vẹn toàn hàm cơ bạn dạng.
Cuối nằm trong, tớ tính tổng những độ quý hiếm của những vẹn toàn hàm đang được tính được để sở hữu sản phẩm cộng đồng của vẹn toàn hàm của hàm số sin nón n x.
Lưu ý: Công thức bên trên chỉ vận dụng mang lại n/2 là số vẹn toàn. Trong tình huống n/2 ko cần số vẹn toàn, cần dùng phép tắc không ngừng mở rộng nhằm tính.

Xem thêm: trong quá trình dịch mã

Công thức được dùng nhằm tính vẹn toàn hàm của sin mặt hàng ngũ x là: ∫sin(nx)dx = -1/n * cos(nx) + C. Trong số đó, n là thông số nhập biểu thức sin(nx), C là hằng số tự tại và ∫ là ký hiệu mang lại vẹn toàn hàm.

Để tính vẹn toàn hàm của hàm số sin căn bình x, tất cả chúng ta hoàn toàn có thể vận dụng công thức tính vẹn toàn hàm của hàm con số giác cơ bạn dạng.
Theo công thức, tớ có:
∫sin²xdx = ∫(1 - cos(2x))/2 dx
Đặt u = 1 - cos(2x), thì du = 2sin(2x)dx
Thay thế những độ quý hiếm đang được mang lại nhập, tớ có:
∫sin²xdx = ∫(1 - cos(2x))/2 dx
= (1/2) ∫du
= (1/2)u + C
= (1/2)(1 - cos(2x)) + C
Vậy, vẹn toàn hàm của hàm số sin căn bình x là (1/2)(1 - cos(2x)) + C, với C là hằng số.

Công thức được dùng nhằm tính vẹn toàn hàm của hàm số sin khối x là:
∫ sin^2(x) dx = ∫ (1 - cos(2x))/2 dx
Ta phân chia nhỏ hàm số sin^2(x) trở nên (1 - cos(2x))/2 nhằm dễ dàng đo lường và tính toán.
Tiếp theo gót, tớ tính vẹn toàn hàm của (1 - cos(2x))/2 như sau:
Đặt t = 2x, tớ đem dt = 2dx.
Khi cơ, vẹn toàn hàm của (1 - cos(2x))/2 là:
(1/2) ∫ (1 - cos(t))/2 dt = (1/2) ∫ (1/2 - (1/2)cos(t)) dt
= (1/4) ∫ (1 - cos(t)) dt
= (1/4) (t - sin(t)) + C
Ở trên đây, C là hằng số tích cực kỳ (constant of integration).
Cuối nằm trong, tớ thay cho lại t = 2x nhập những công thức bên trên để sở hữu sản phẩm cuối cùng:
(1/4) (2x - sin(2x)) + C

Để tính vẹn toàn hàm của hàm số sin bình phương x, tất cả chúng ta hoàn toàn có thể dùng công thức tính vẹn toàn hàm của những nồng độ giác cơ bạn dạng.
Công thức chủ yếu nhằm tính vẹn toàn hàm của hàm sin bình phương x là:
∫ sin^2(x) dx = ∫ (1 - cos(2x))/2 dx
Chúng tớ hoàn toàn có thể trả về dạng này bằng phương pháp dùng công thức hạ bậc và công thức hoạn lượng giác.
Bước 1: sít dụng công thức hoạn lượng giác: sin^2(x) = (1 - cos(2x))/2
Bước 2: Tính vẹn toàn hàm của đại lượng (1 - cos(2x))/2:
∫ (1 - cos(2x))/2 dx = ∫ (1/2 - cos(2x)/2) dx = (1/2)∫ dx - (1/2)∫ cos(2x) dx = x/2 - (1/2)∫ cos(2x) dx
Bước 3: Tính vẹn toàn hàm của cos(2x):
∫ cos(2x) dx = (1/2)sin(2x) + C
Với C là hằng số nằm trong.
Bước 4: Kết hợp ý những sản phẩm của bước 2 và bước 3:
∫ (1 - cos(2x))/2 dx = x/2 - (1/2)∫ cos(2x) dx = x/2 - (1/2)(1/2)sin(2x) + C = x/2 - (1/4)sin(2x) + C
Vậy, vẹn toàn hàm của hàm số sin bình phương x là x/2 - (1/4)sin(2x) + C.
Chú ý: Tại trên đây, C là hằng số nằm trong tự tại và hoàn toàn có thể được lựa chọn theo gót ý ham muốn.

Công thức được dùng nhằm tính vẹn toàn hàm của lượng giác bình phương x là:
∫sin^2(x)dx = ∫(1 - cos(2x))/2 dx
Với việc vận dụng công thức hạ bậc, tớ thay cho thế sin^2(x) vì chưng (1 - cos(2x))/2.
Để tính vẹn toàn hàm này, tớ hoàn toàn có thể sử dụng cách thức thay cho thế hoặc dùng công thức nằm trong hoặc trừ, tuỳ ý.

Để tính vẹn toàn hàm của cos khối x, tớ hoàn toàn có thể vận dụng những công thức và quy tắc tính vẹn toàn hàm. Dưới đấy là công việc cụ thể nhằm tính vẹn toàn hàm của cos khối x:
Bước 1: Xác tấp tểnh hàm số cần thiết tính vẹn toàn hàm. Trong tình huống này, hàm số cần thiết tính vẹn toàn hàm là cos khối x.
Bước 2: Xác tấp tểnh đổi mới số và mò mẫm công thức vẹn toàn hàm ứng với hàm số cơ. Với cos khối x, tớ đem công thức vẹn toàn hàm là sin khối x.
Bước 3: Ghi công thức vẹn toàn hàm này lại. Với hàm số cos khối x, vẹn toàn hàm của chính nó là sin khối x.
Bước 4 (tuỳ chọn): Kiểm tra sản phẩm bằng phương pháp lấy đạo hàm của vẹn toàn hàm một vừa hai phải tính. Nếu đạo hàm của vẹn toàn hàm cơ vì chưng hàm số gốc, tức là cos khối x, thì sản phẩm đo lường và tính toán là đúng đắn.
Ví dụ: Để tính vẹn toàn hàm của cos khối x, tớ đem sản phẩm là sin khối x.
Nguyên hàm của cos khối x là sin khối x (C).
Lưu ý: Việc đo lường và tính toán vẹn toàn hàm hoàn toàn có thể phức tạp rộng lớn so với những hàm số phức tạp rộng lớn. Hoặc nhập một vài tình huống, hoàn toàn có thể ko thể mò mẫm ra sức thức vẹn toàn hàm cho 1 hàm số ví dụ. Trong tình huống này, tớ hoàn toàn có thể dùng những cách thức khác ví như tích phân số học tập nhằm tính tầm vẹn toàn hàm của hàm số cơ.

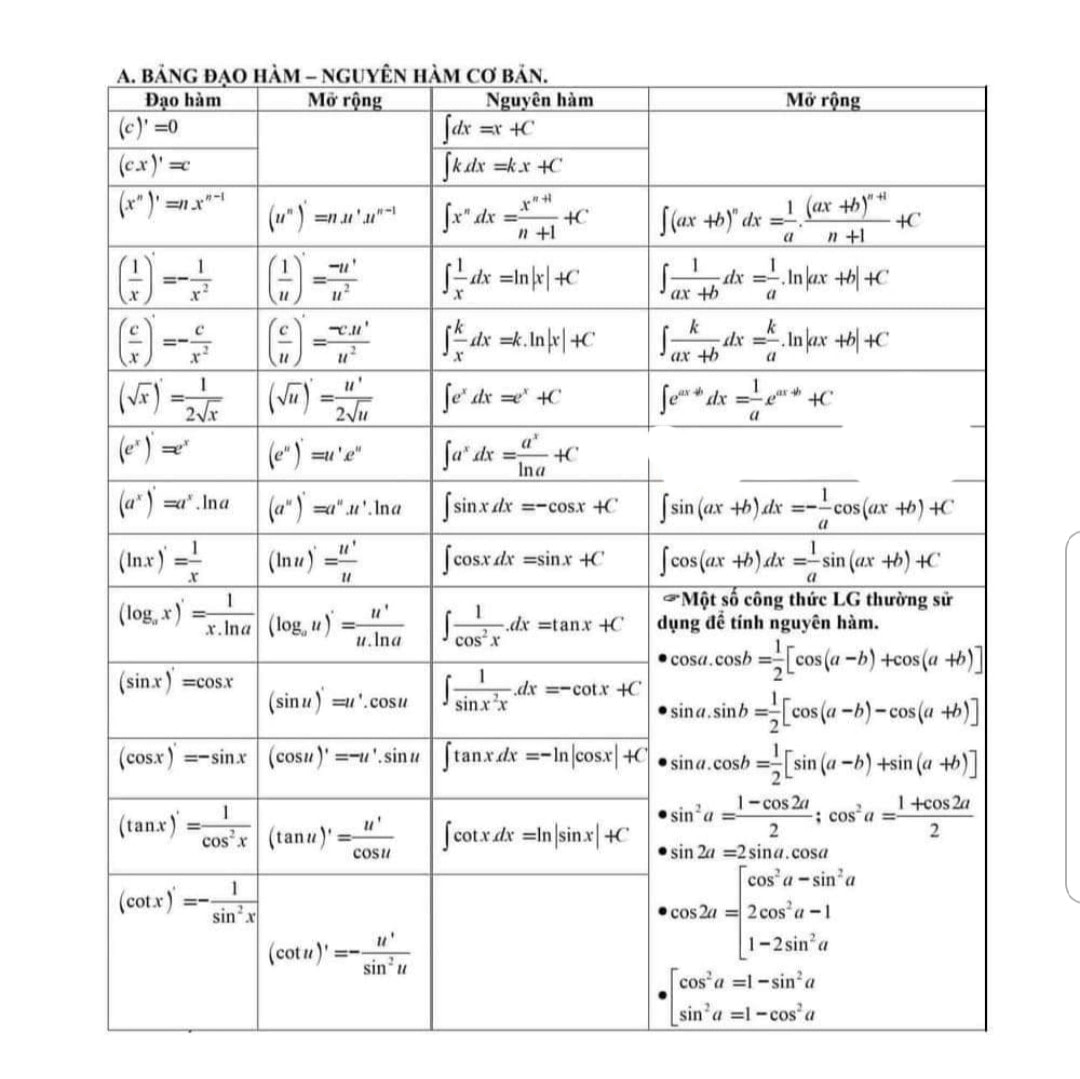
Xem thêm: tác dụng của biện pháp liệt kê

Công thức được dùng nhằm tính vẹn toàn hàm của hàm số cos bình x là:
∫ (cos^2 x) dx = ∫ (1 + cos(2x))/2 dx
Bước thứ nhất, tất cả chúng ta dùng công thức phân chia mảng tưng bức nhằm phân tan hàm số cos bình x trở nên những bộ phận tương tự rộng lớn. Ta tiếp tục dùng công thức sau đây:
cos^2 x = (1 + cos(2x))/2
Sau cơ, tớ tính vẹn toàn hàm của từng trở nên phần:
∫ (1 + cos(2x))/2 dx = (1/2) ∫ 1 dx + (1/2) ∫ cos(2x) dx
Đối với bộ phận thứ nhất, tớ có:
∫ 1 dx = x + C1
Đối với bộ phận loại nhì, tớ dùng quy tắc tính vẹn toàn hàm của cosine:
∫ cos(2x) dx = (1/2) sin(2x) + C2
Cuối nằm trong, tớ phối kết hợp nhì bộ phận lại nhằm tính vẹn toàn hàm cuối cùng:
∫ (1 + cos(2x))/2 dx = (1/2) (x + C1) + (1/4) sin(2x) + C2
Vậy, vẹn toàn hàm của hàm số cos bình x là:
(1/2) (x + C1) + (1/4) sin(2x) + C2

Để tính vẹn toàn hàm của hàm số cos nón n x, tớ hoàn toàn có thể dùng công thức hạ bậc hoặc công thức đặc biệt quan trọng. Dưới đấy là phương pháp tính chi tiết:
Cách 1: Sử dụng công thức hạ bậc
- Trường hợp ý n không giống 0:
+ Ta bịa đặt u = cosⁿx và dv = d(x).
+ Tính đạo hàm của u và tích phân của dv nhằm mò mẫm du và v.
+ sít dụng công thức tích phân theo gót thành phần nhằm tính vẹn toàn hàm:
∫cosⁿxdx = cosⁿ₋¹x.sinx/ⁿ+(ⁿ⁻¹/ⁿ)∫cosⁿ₋²x.dx
+ Sử dụng công thức bên trên tái diễn mang lại ∫cosⁿ₋²x.dx nhằm tính tiếp vẹn toàn hàm mang lại cosⁿ₋²x và nối tiếp cho tới Khi tớ tính được vẹn toàn hàm của hàm số thuở đầu.
- Trường hợp ý n = 0:
+ Ta đem cos⁰x = 1, tự đó:
∫1.dx = x + C
Cách 2: Sử dụng công thức quánh biệt
- Dùng công thức tổng quát:
∫cosⁿx.dx = (∫cosx.dx) / (∫cos²x.dx)
Trong đó:
+ ∫cosx.dx = sinx + C₁
+ ∫cos²x.dx = ∫(1 + cos2x)/2.dx = ∫(1/2).dx + (∫(cos2x)/2.dx)
= (1/2)x + (1/4)sin2x + C₂
- Kết hợp ý nhì công thức bên trên, tớ tính được vẹn toàn hàm của hàm số thuở đầu.
Các công thức bên trên đơn thuần một vài cách thức tính vẹn toàn hàm của hàm số cos nón n x. Còn tùy thuộc vào độ quý hiếm của n và từng tình huống ví dụ, hoàn toàn có thể vận dụng những công thức không giống nhằm tính vẹn toàn hàm.